Basketball players perform many hours of shooting drills and training in order to improve their shooting percentage. However, questions remain regarding how shot release conditions and strategy relate to performance. Shooting a basketball is more complex than simply identifying one optimal release since it’s a redundant task resulting in an infinite set of successful release conditions. This redundancy requires the shooter to navigate a solution space and balance factors such as motor variability, minimization of error, and a complex sequence of joint coordination to determine the best action. Investigations into how the shooting release is regulated (Robins et al., 2006; Bartlett et al., 2007; and Button et al., 2003) have found that joint angle variability along the proximal-distal kinematic chain at release had no adverse effect and may serve as a compensatory functional variation. Mullineaux and Uhl (2010) proposed that the observed coordination-variability near release may indicate that participants perceive a difference between their motion and desired release and dynamically correct. This suggests that individuals select a desired release condition and dynamically adjust to achieve it rather than simply repeating a desired motion.

How skilled basketball shooters select their preferred shot release velocity and angle from among the redundant solution remains a debated topic with differences stemming from the assumed relationships regarding velocity, motor noise, and release error. Early studies proposed a minimum velocity release to minimize energy expenditure (Brancazio, 1981; Miller and Bartlett, 1993). The role of sensorimotor noise in redundant tasks and its proportionality with force and velocity have been widely recognized (Bays and Wolpert, 2007; Faisal et al. 2008) and further led to speculation that shooting strategies using minimum release velocities are preferred by decreasing velocity-dependent motor noise, resulting in greater movement consistency (Okazaki et al., 2015).

In contrast, Sternad et al. (2011) have shown that in similar throwing tasks, participants chose maximum error-tolerant over minimum velocity strategies and didn’t find any velocity-dependent increase in variability. Additional nondeterministic studies treating the shooter as a probabilistic system (Hamilton and Reinschmidt, 1997; Tran and Silverberg, 2008) have found that release conditions maximizing probability are different than those minimizing release velocity and dependent on the ratio of intra-individual release velocity and angle standard deviations (SD) (Gablonsky and Lang, 2005). Therefore, any discussion regarding shooting strategy must carefully consider release velocity and angle SD. Nakano et al. (2020b) integrated the minimum velocity and maximum probability strategies by assessing sensitivity to error propagation. They proposed that an error-tolerant strategy balancing release velocity error and angle error was preferred and resulted in a near-minimum release velocity strategy.

How release velocity and angle SDs are related to distance, force generation, and shooting performance remains an outstanding question important for future investigations regarding performance and learning. If velocity-dependent motor noise dominates the shooting process, as distance increases, experiments should demonstrate a proportional increase in release velocity and angle SDs. Independence of release conditions with release velocity, however, may suggest strategies rely more strongly on maximizing probability. Intra-individual changes in release velocity and angle are the most relevant parameters in evaluating velocity-dependence since they isolate changes within an individual as distance changes. Inter-individual and group parameters, however, show differences among individuals and due to different release heights and shooting patterns, may be larger than more subtle changes within an individual.

Existing results remain mixed with studies reporting wide ranges in SDs of release velocities spanning 0.3-0.65 m/s for free throws and 0.2-0.8 m/s for three-point shots (Okazaki and Rodacki, 2012; Miller and Bartlett, 1993; 1996; Rojas et al., 2000; Robins et al., 2006). In contrast, through simulation, Silverberg et al. (2018) showed that for a 70% free throw shooter the required velocity SD should be 0.095 m/s, much smaller than those reported experimentally. The large discrepancy in results may stem from multiple sources: a) studies having measurement errors larger than the actual velocity SD and masking the trends in question, b) studies reporting SDs for only made attempts (Robins et al., 2006), and c) reporting group and inter-individual SDs rather than intra-individual SDs (Rojas et al., 2000; Okazaki and Rodacki, 2012).

There is a need to address the differences between simulated and experimental shooting release conditions and the lack of reported intra-individual release velocity and angle SDs. These differences for both free throws and three-point shots are important since they require different release velocities, forces, and levels of energy transfer from the lower limbs to the shooting arm. Such research may provide valuable insights into how minimum velocity and maximum probability shooting strategies interact and the role of velocity-dependent factors. Therefore, this study aims to analyze how intra-individual release velocity and angle SDs are related to distance and shooting performance among skilled basketball players. The study hypotheses are: (1) release velocity and angle SD are independent of distance and shot type, and (2) shooting performance is effectively predicted by an individual’s release velocity SD.

Twelve male participants (n = 12), who had competitive experience at secondary (n = 6) or collegiate level basketball (n = 6), were recruited for this study. None of the collegiate level participants were within their competitive season at the time of the study. The mean (± standard deviation) age and height of the participants were 24.5 ± 7 years and 185 ± 9 cm, respectively. The participants were all considered skilled shooters and had free throw shooting percentages of 79 ± 11% during the study, slightly higher than the historic collegiate average of 69% (c.f. participants in the study of Nakano et al. (2020a): 67 ± 18% and Button et al. (2003): 62%). Each participant gave their voluntary consent for inclusion in the study, which was approved by the local ethics committee.

Participants were asked to take a series of shots on a regulation height hoop (H = 3.05 m) from both the NCAA men’s three-point line (L = 6.75 m) and a regulation free throw line (L = 4.19 m). Each participant completed five sets of 15 three-point shots followed by 10 free throws for a total of 75 three-point shots and 50 free throws. All shots were attempted centered and perpendicular to the backboard. The participants could freely set up each shot in a manner they felt most natural. The only requirement was that their feet had to be behind the designated distance markers when shooting. After each attempt, participants retrieved their shot and returned to the designated distance to set up their next attempt. All participants, without instruction, shot free throws by dribbling in place and shooting without leaving the ground. In contrast, all participants attempted three-point shots by starting a few steps behind the marker, dribbling into the shot, and leaving the ground while jumping.

Each shot was recorded using a tripod-mounted 60 fps Panasonic HC-VX870K 4K digital video camera placed perpendicular to the sagittal plane, 6 m from the shooter, 1.5 m above the surface, a distance L from the center of the hoop, and a shutter speed of 1/500 seconds. Image resolution was 1920 x 1080 and the focal length was set so that approximately 3.1 m of the sagittal plane appeared in the image resulting in less than 2 mm per pixel. Two 91.5 cm high-contrast calibration sticks were placed along the floor in the sagittal plane in order to relate global distances to pixels. The sticks were placed 50 cm in front of the three-point and free throw lines, respectively.

The global coordinate system used is defined in Figure 1 where, the center of the hoop is at a location (0, H). Each shot was analyzed using Tracker 5.1.5 software (Open Source Physics Java framework). The initial global coordinate location of the ball’s geometric center, also its center of gravity (CG), was identified as the instant the shooter lost contact with the ball and no longer imparted acceleration. As shown in Figure 1 the initial location of the ball is (x_*– L, y_*). Due to arm extension, release angle, variability in shot location, and forward jumping, x_* could vary substantially between shots. The ball’s trajectory was then identified by manually locating the ball’s center in subsequent frames. A 25 mm marker was also placed on each participant’s right iliac crest and used to approximate the body’s mass center. The iliac crest was manually tracked from its lowest position to the point where the shooter lost contact with the ball.

The sensitivity of ball release velocity, v₀, and release angle, θ¸₀, to estimation methodology has often been overlooked in previous studies. In particular, an estimation process must ensure that variability in ball location from frame to frame does not contribute more to the estimated velocity and angle variation than the shooter. As noted earlier, previous studies (Okazaki and Rodacki, 2012; Miller and Bartlett, 1993; 1996; Rojas et al., 2000) have reported SDs in release velocities for three-point shots ranging from 0.36-0.8 m/s, which are almost an order of magnitude larger than expected based on reported make percentages and numerical simulations. In such cases, it’s suspected that the estimation process may largely contribute to the reported SDs.

To illustrate the challenge in estimating v₀ and θ¸₀, consider the simplest kinematic method where only a few ball CG locations near release are used. Velocity can be found by multiplying displacement by the frame rate. However, for fast frame rates, even small variations in location estimates result in significant changes. Reduction in sensitivity to ball CG estimates can be achieved by using frames separated by more time, however, estimates for the release angle would be adversely affected since the path’s curvature and velocity reduction from drag would contribute to errors. These limitations are present in both video and motion capture systems.

An essential tool for minimizing estimation error of a shot release is the development of an accurate and preferably analytic ball trajectory model to provide robust filtering of raw measurements, ensure kinematic consistency, and reduce noise. Development of the model begins by recognizing that once the ball is released, only gravity and aerodynamic forces remain. The shooting process can be treated as the shooter attempting to achieve an initial release velocity, v₀, and angle, θ¸₀, based on their distance from the basket so that the ball goes through the basket. The equation governing the motion of the basketball after release is

where v = v_xi + v_yj and a = v_xi + v_yj are the ball’s velocity and acceleration, f_W = – (m_a + m_b)gj and f_B = m_agj are the weight and buoyancy forces, and m_b, m_a, and m_t, are the mass of the ball, the air inside the ball, and the total combined mass, respectively. Using a conventional projectile drag model, drag can be written as

where D is the ball’s diameter, 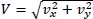is the total speed, and C_D is the drag coefficient. Combining force components with (1) results in the following two nonlinear coupled differential equations

where m^' = m_b/m_t.

Solutions to (3) and (4) can be found by numerical integration as in Silverberg et al. (2003) and Okubo and Hubbard (2006), however, numerical solutions are not conducive to parametric analysis. Approximate solutions to (3) and (4) have been proposed by many authors. The most common technique is to assume that the drag force is small compared to the combined weight and buoyancy forces so that drag can be neglected altogether. This may be quantified by defining the drag to weight ratio as

so that if R_DW is small, the drag in (3) and (4) may be neglected. In such a case (3) and (4) become two decoupled linear differentials with the well-known parabolic projectile solution. However, they only approximate the general solution when the velocity is small, and the mass is large compared to the object’s diameter. For a standard men’s basketball with D = 0.241 m, m_b = 0.624 kg, C_D = 0.5, and a three-point initial velocity of 8.8 m/s, the resulting R_DW is 0.18, approaching nearly 20% of the total force.

An improved approximate solution incorporating drag can be found using techniques employed by the exterior ballistics literature where it’s often assumed that if the velocity is very high or the velocity range is small (the latter applicable to basketball), C_D can be accurately approximated by k/V, where k is a known constant. Applying this approximation and defining the ballistic coefficient

as a known constant, (3) and (4) become two decoupled linear differential equations with the following analytic trajectory solution:

To demonstrate the importance of drag, trajectories for both a three-point shot and free throw using a no drag parabolic model and the proposed C_D = k/V model (6-7) are compared with numerical integration of (3) and (4). Figure 2 shows all three trajectories for a shot released 6.56 m from the center of the basket for a three-point shot and 4.00 m for a free throw, both from a height of 2.54 m. In order to pass through the hoop, the three-point shot is released with a velocity of 8.76 m/s and an angle of 48 degrees, while the free throw is released with a velocity of 6.93 m/s and an angle of 48 degrees. From Figure 2 it’s clear that neglecting drag results in significant trajectory errors while the approximation C_D = k/V provides an excellent approximation to the full model. The maximum trajectory errors for the proposed model with C_D = k/V are an order of magnitude smaller than the conventional no drag models often used. For the three-point shot, maximum errors in trajectory, time of flight, and final approach angle are only 2.6 cm, 6 ms, and 0.4 degrees, respectively, for the proposed model, while they grow to 53.1 cm, 45 ms, and 2.2 degrees for the no drag model.

In this study, long trajectory segments spanning multiple ball CG estimates along with the proposed trajectory model are used within a least squares estimator to improve estimates of the initial position (x₀, y₀), v₀, and θ¸₀. This decreases overall sensitivity to variations in individual ball CG locations, while also compensating for the effects of drag.

To form the least squares estimator, the analytic trajectory approximations found in (6) and (7) are written as two scalar nondynamic systems

where xÌ‚ and yÌ‚ are vectors to be estimated. Measurements, x̃ and ỹ, due to noise, will not uniquely satisfy (8) and (9). Rather, for n measurements, the scalar equations can be placed in the matrix form with x̃ and ỹ being n x 1 measurement vectors from the left side of (8) and (9) and H being an n x 2 matrix formed by concatenating [1 (1 - e^-βt_θ¹)/β]. Using vector calculus, estimates for xÌ‚ and yÌ‚ which minimize the error become (H^TH)^-1 H^T x̃ and (H^TH)^-1 H^Tỹ, respectively.

The robustness of the proposed least squares estimator (LSE) incorporating the analytic drag model is assessed by comparing estimates of v₀ and θ¸₀ to those of a simpler two-point kinematic method as the estimated initial CG location is varied. A three-point shot that resulted in a make with no rim contact was selected as the baseline case considering the final location is known. The two-point method used i =1 and 3 in Figure 1 and estimates v₀ using a finite difference approach while assuming a no drag straight-line trajectory to estimate θ¸₀. The proposed LSE used ten CG locations (i = 1-5, 13-17). Using the same identified CG locations (original), Table 1 shows that both estimates are similar. However, when the initial CG location is moved left by 1.0 cm (4% of the ball’s diameter) the LSE method changes by only 0.01 m/s (<0.1%) and 0.1 degrees (0.2%). In contrast, the two-point method results in a change of 0.21 m/s (2.4%) in v₀ and -1.4 degrees (3.0%) in θ¸₀. The sensitivity of the two-point method, and robustness of the LSE method, are further illustrated by showing how the trajectory solution for the final distance reached (x_F) at rim level changes. Table 1 shows that even after the initial CG location was changed, the LSE x_F distance only varied by 1.1 cm. However, for the two-point method, the original data results in the shot missing by 21.2 cm short, and with the CG changed by only -1.0 cm it’s then long by 10.4 cm and can’t reliably predict the shot result and has a variation in v₀ comparable to that of a potential shooter.

Another source of variation in estimates of v₀ that must be considered is the shooter’s position relative to the desired distance line. While the shooter is aware of the line, it was observed for three-point attempts that the participants would shoot within a range of 0 to 30 cm behind the line (free throws had considerably less variation). If two made shots are released from slightly different distances (or heights) the velocities would change. However, their differences cannot be considered an error since in both cases they perfectly achieved their desired release. To isolate the shooter’s error in velocity from their variation in release position, normalizing each shot to a common distance using the gradient of required initial velocity, v₀, with respect to the distance x_* and y_* is required.

The required gradients are found by first eliminating time from the trajectory equations in (6) and (7) then specifying the successful shot boundary conditions, (x₀, y₀) as (x_* – d, y_*) and (x, y) as (0, H). The resulting solution is

describing the required release velocity, v₀, to reach the center of the basket from (x_*– d, y_*) when shot at an angle θ¸₀. Differentiating (10) with respect to x_* and y_* results in the desired gradients

providing analytic solutions to the variation in required v₀ as the shooter varies their release. In the results that follow all velocities reported are compensated to a common longitudinal position according to

where, v_est is the velocity from the estimator and x̄_* and ȳ_* are the means of x_* and y_*.

The importance of (12) is illustrated by considering a three-point shot released 6.56 m from the center of the basket, at a height of 2.54 m, and 48 degrees, resulting in a σθ½_* of -0.65/s. A shot made from 30 cm behind the line requires a velocity 0.195 m/s higher than if shot from the line. Failure to compensate for this variation would lead to any reported release velocity statistics being dominated by release position variation and not the shooter’s accuracy. When both the potential estimator error and release position variations are combined, they approach the reported release velocity SDs of 0.2-0.8 m/s in the existing literature (Okazaki and Rodacki, 2012; Rojas et al., 2000; Robins et al., 2006). This suggests that those reported values may include both sources of error in addition to the subject’s error, and thus the statistical quantity attempting to be measured may be dominated by other factors.

Global data for each shot was processed using the LSE and compensated for distance variation. Statistical analysis was performed in Matlab v9.2.0 R2017a (Mathworks Inc., Natick MA, USA). Descriptive statistics are presented as means and SDs for inter-individual data: release velocity v₀; release angle θ¸₀; mass center movement ∆X, ∆Y, (V_X)_max, (V_Y)_max and intra-individual data: release velocity v₀ SD; release angle θ¸₀ SD. Paired t-tests among free throws and three-point attempts were used for inter-participant (all participants) statistics. Intra-participant analysis used the nonparametric Wilcoxon signed-rank test rather than a standard t-test due to its robustness to outliers. Due to the sample size being less than twenty an exact p-value using enumeration is found for all intra-individual rather than a normal approximation. Analysis of each linear regression is presented using the Pearson product-moment coefficient, r. Statistical significance was set at 0.05.

The participants’ mass center movements while shooting were measured by tracking the motion of the iliac crest. Table 2 shows changes in displacement within the sagittal plane from the shooters’ lowest to highest points and the maximum velocities. As participants moved from a free throw to a three-point shot, release velocity increased from 7.02 m/s to 8.71 m/s (p < 0.001). Vertical (∆Y and (V_Y)_max) and horizontal (∆X and (V_X)_max) mass center motion also increased as distance increased (p < 0.001). Accompanying the increase in velocity and lower-limb mobility as distance increased was a 3.3 degree reduction in release angle (p = 0.001). All results in Table 2 represent inter-individual statistics. The variable v₀ = 8.71 m/s for three-point shots indicates the average of all individual mean release velocities with ±0.14 m/s representing SD of individual means. Such a SD is indicative of a group statistic rather than the SD of any individual. In contrast, the three-point v₀ SD of 0.089 m/s in Table 2 is the mean SD of all individuals and represents a true inter-individual SD. The significance of ±0.14 m/s (SD of mean release velocity) being large than 0.089 m/s (mean of individual release SDs) is that differences in individual release velocity conditions are larger than each individual’s own velocity SD.

Intra-individual changes in each participant’s release velocity SD from free throws to three-point attempts (positive indicating three-point SD is larger) are presented in a box plot shown in Figure 3(a). Most participants exhibit only marginal changes in release velocity SD as distance and release velocity are increased. These changes are significantly smaller than their velocity SD and are near the median of 0.0025 m/s except for three outliers. A Wilcoxon signed-rank test results in a p-value of p = 0.47 and a 95% confidence interval of 0.010 to -0.005 m/s demonstrating no significant difference is observed in the intra-individual free-throw and three-point release velocity SD.

The box plot in Figure 3(b) shows that nine of the twelve participants decreased their release angle SD as distance increased. A Wilcoxon signed-rank test results in a p-value of p = 0.088 and a 95% confidence interval of 0.02 to -0.35 m/s. Though not conclusive, the p-value is suggestive (0.05 < p < 0.10) of a trend that many shooters may refine their release angle pattern further from their target rather than increasing deviation as release velocity is increased.

Intra-individual release velocity SD along with shooting accuracy for each of the twelve participants are shown in Figure 4. As a participant’s velocity SD decreases for free throws and three-point shots, their shooting accuracy increases. Linear regressions for both three-point shots and free throws (Figure 4) along with the Pearson product-moment coefficients reveal a strong correlation between velocity SD and make percentages for both distances (r = -0.96, p < 0.001 for three-point shots, and r = -0.88, p < 0.001, for free throws). Numerical predictions from Silverberg et al. (2018) for a 70% free throw shooter are shown by an “*” in Figure 4 and closely match the measured results.

Figure 4 also illustrates how the measured range of velocity SD for both free throws and three-point shots are similar, falling within a range of 0.05-0.13 m/s, with lower SD corresponding to better shooters. Results fail to identify any significant increase in the release velocity SD as shooters transition from a free throw to a three-point shot despite the observed increase in lower body motion. Rather, the trend lines show a horizontal shift to the left, not up, with the three-point curve shifted to the left by 20%. Figure 5 further illustrates this phenomenon, where each participant’s free throw and three-point release velocity SD pair is identified and connected with a dashed line. This depicts the independence of release velocity SD with distance as most shooters show a horizontal shift with little to no change in release velocity SD as they move further from the hoop.

Unlike the release velocity SD, release angle results in Figure 6 reveal a very weak negative relationship between shooting performance and release angle SD for three-point shots (r = -0.408, p = 0.19) and a moderate negative correlation for free throws (r = -0.69, p = 0.02). Regardless of the shot type, most of the participants’ release angle SD occur within 0.8 to 1.6 degrees.

An important feature of this study was the ability to measure the release velocity and angle with sufficient accuracy as to allow meaningful analysis of intra-individual changes. The observed 0.05-0.13 m/s range of release velocity SD was significantly lower than the 0.3-0.65 m/s for free throws and 0.2-0.8 m/s for three-point shots reported by earlier studies (Okazaki and Rodacki, 2012; Miller and Bartlett, 1993; 1996; Rojas et al., 2000; Robins et al., 2006) and are more consistent with numerically predicted values by Tran and Silverberg (2008). Studies reporting group and inter-individual results similar to v₀ in Table 2 (Okazaki and Rodacki, 2012; Miller and Bartlett, 1993; 1996) report release velocity SDs significantly higher (0.5-0.65 m/s for free throws, 0.62-0.8 m/s for three-pointers) than found in this study (0.15 m/s for free throws, 0.14 m/s for three-pointers) with previous studies showing an increase as distance increased. Studies by Robins et al. (2006) and Mullineaux and Uhl (2010) report release velocity SDs most similar to those presented here. The inter-individual release velocity SD reported by Robins et al. (2006) are 0.3 m/s and 0.17 m/s for free throws and three-point shots, respectively, and decrease with distance. However, it must be noted that these are only for made shots and don’t suggest that an individual’s release velocity SD decreases for all shots. Rather, as distance is increased, a made shot requires more precision due to larger interactions between the ball and rim. For example, a free throw shot that may graze the rim and roll in, may ricochet off for a three-point attempt. Mullineaux and Uhl (2010) report inter and intra-individual free throw release velocity SD values most similar to those found in this study (0.06-0.15 m/s). A direct comparison is difficult, however, since they don’t directly measure a release velocity but derive an optimal speed and angle from the measured release position. Such a statistic more accurately reflects a shooter’s consistency in repeating a release location rather than their release velocity.

Results in this study illustrate that as distance and shooting style changed from free throws to three-point shots, the required ball release velocity increased 24% and lower limb displacement and velocity significantly increased. These results are in agreement with other studies showing that as distance increases, joint work in the lower limbs increase significantly (Nakano et al. 2020a). Podmenik et al. (2017) and Okazaki and Rodacki (2012) have also shown that as distance increases, joint angular velocities also significantly increase. Combined, these illustrate that as shooting distance increases, release and limb velocities also increase. Therefore, if velocity-dependent effects are present in shooters’ strategies they should manifest themselves in intra-individual changes as the shooting distance is increased. However, results show, that unlike previous studies, neither intra-individual release velocity SD nor angle SD increased from free throws to three-point attempts and velocity-dependent effects are absent. Therefore the first hypothesis: release velocity and angle SD are independent of distance and shot type, is accepted.

These findings provide important information for future work investigating shooting performance and learning. Since the release velocity and angle SD are independent of velocity-dependent factors such as distance and lower-limb activity, velocity-dependent motor noise may not be a primary factor in basketball shooting strategies. These findings agree with results from Sternad et al. (2011) for general throwing tasks, where they found participants chose error-tolerant over minimum velocity strategies and observed that velocity-dependent variability was absent. The findings in this study provide support for similar theories that propose basketball shooting strategies are primarily driven by minimizing sensitivity to error and not velocity-dependent motor noise such as Nakano et al. (2020b). Earlier studies showing how shooters use functional compensation late in the shot to minimize release errors (Button et al., 2003; Robins et al., 2006; Bartlett et al., 2007), and links between distal joint proprioception and shooting performance (Sevrez and Bourdin, 2015) may account for the observed ability to maintain similar release SDs even as distance increases.

Another important finding of this study was that shooting percentage was primarily correlated with the release velocity SD with only a weak dependence on release angle SD (Figures 4-6). Therefore, the second hypothesis: shooting performance is effectively predicted by an individual’s release velocity SD, is accepted. The decrease in make percentage while the release velocity SD remains fixed may come from two sources. First, as shooting distance increases, the sensitivity to sagittal plane release error (directional error) amplifies. Second, due to higher release velocities, impact velocity increases at the hoop, reducing the probability of making an imperfect shot, similar to why the SD in Robins et al. (2006) for made attempts decreases as distance increases.

A compelling finding of this study is that since release velocity SD is independent of shot type and distance, and release velocity deviation is directly related to shooting performance, a shooter’s accuracy may be best understood as being primarily dependent on their ability to control release velocity deviation. Although a simplification of a complex process, this perspective has the potential to revolutionize shooter development. Training that improves elbow-wrist control and distal joint proprioception may have more impact on performance than traditional training methods which attempt to develop a highly repeatable motion. These results point to the value in further studies identifying and developing drills and training exercises that can demonstrate efficacy in refining a shooter’s release velocity control. One potential method to achieve results with less repetition may be to place greater training emphasis on feedback from visual cues related more directly to release velocity rather than focusing on the shooter’s attention to particular body motions.

This article, in contrast to many earlier studies, has shown that even as shooting distance and force are increased, the resulting intra-individual release velocity SD remains unchanged. The absence of any velocity-dependent changes indicates that motor-noise may not be a limiting factor in basketball shooting performance. Rather, performance is almost exclusively determined by a shooter’s ability to control their release velocity SD. Since, over a wide range of conditions, shooters are able to preserve their release velocity SD, it’s suggested that their performance may be dictated by the ability to compensate for variability using elbow-wrist joint proprioception. From a practical standpoint this article suggests that, in addition to traditional training, shooting performance may benefit from new methods which exercise the ability to compensate for joint errors and process proprioceptive information.