Within professional soccer, the quantification of both internal and external training loads holds a key role for tailoring training procedures to individual needs, with the ultimate goals of averting fatigue, mitigating the risk of illness and injury, and optimizing performance outcomes (Jones et al., 2017; Impellizzeri et al., 2023; Akenhead and Nassis, 2015). In this context, the term "internal load" pertains to an individual's psychophysiological response to the external load (Schwellnus et al., 2016; Soligard et al., 2016). Internal load parameters encompass factors like ratings of perceived exertion (RPE) and heart rate, while parameters such as the distance covered and accelerations are parameters of external load.

Despite the importance of monitoring internal and external load, there is no universally adopted monitoring approach in high-level soccer (Akenhead and Nassis, 2015). More than 50 different external and internal load parameters are assessed in different high-level soccer clubs, and most soccer clubs employ external load parameters (Akenhead and Nassis, 2015). This is surprising, since it was recommended to use internal load parameters over external load parameter athletes where possible (Impellizzeri et al., 2019) and that subjective self-reported parameters trump commonly used objective parameters (Saw et al., 2016). If external load is measured more easily than internal load, but internal load (and specifically subjective parameters) is of relevance, the relationship between external and internal load markers must be understood to optimize training procedures of athletes and to monitor an athlete's response to external load (McLaren et al., 2018).

Research endeavors have been undertaken to investigate the relationship between external and internal load parameters and we refer readers to existing articles (e.g. (Bourdon et al., 2017; McLaren et al., 2018). This research has advanced our understanding of the relationship between internal and external load and provide valuable insights to coaches for the purpose of planning training sessions. However, the majority of available original research has investigated relationships of few selected internal and external parameters, and left others out, thereby potentially missing important relationships between internal and external parameters. One reason for this is maybe employed statistical approaches are unsuitable for the inclusion of many parameters – a problem which can be overcome by machine learning and artificial intelligence techniques (Bishop and Nasrabadi, 2006). While still being scarcly used, the applications of years machine learning and artificial intelligence techniques are increasing for revealing the relationship between external parameters and e.g. different forms of RPE (Vandewiele et al., 2017; Jaspers et al., 2018; Vallance et al., 2023; Bartlett et al., 2016).

While this research has advanced our understanding of external load markers with RPE, current approaches revealing relationships between RPE and other internal and/or external load parameters are not without limitations and can be improved. For example, findings of Vandewiele et al (2017) cannot be generalized to other individuals then the once used in the respective study, since the machine learning algorithms incorporated individual data such as e.g. age or playing position (Vandewiele et al., 2017).

In order to advance the current body of literature and uncover the relationship between various external and internal load parameters and RPE, the main article aim of this article is to identify the relationship between external and internal load parameters with subjective RPE. Additionally, these relationships shall be used to design machine learning and deep learning architectures to predict RPE based on other internal and external load parameters. Predicting RPE based on other internal and external load parameters might be useful for coaches e.g. if the athlete-reported RPE is missing due to low compliance or for comparing the reported RPE with the predicted RPE. Such a comparison is beneficial for identifying discrepancies that might indicate increased athlete fatigue (if the athlete-reported RPE is higher than the predicted RPE) or improved athlete "fitness" (if the athlete-reported RPE is lower than the predicted RPE). Additionally, coaches might use our algorithms to plan training more precisely in order to avoid differences between planned RPE values by coaches and perceived RPE by athletes (Inoue et al., 2022). Consequently, the secondary aim of our article is to assess the performance of various machine learning models and deep learning architecture for predicting RPE using objectively measured external and internal load parameters.

26 healthy male national level soccer players (Tier 3 level according to a performance framework by (McKay et al., 2022)) of a professional German third division soccer team were recruited for this study (age: 23.2 ± 3.4 years, height: 184 ± 7.2cm, mass: 78.9 ± 8.9kg). All participants gave their written informed consent. As all data used for calculations in this study were collected through daily monitoring, no ethical approval was required (Winter and Maughan, 2009).

During every training session (n = 5402) and each match (n = 732) of the 2019/2020 season, all players were equipped with a sensor of the Polar Team Pro System (Polar Electro Oy, Kempele, Finnland) to monitor heart rate data (60 Hz), accelerometry (100 Hz), and GPS-derived data (10 Hz). Each player was mandated to self-assess their RPE using a standardized 0-10 scale within an hour after every training session or match. During regular seasonal testing procedures of players, their individual maximal heart rate was determined in a standardized incremental test (starting at 7 km·h^-1, increasing by 1 km·h^-1 every minute) performed on a treadmill until full volitional exhaustion. Heart rate was measured using a Polar H10 sensor.

Our analysis involved the calculation of 174 parameters (referred to as features) derived from GPS-units, heart rate sensors, and inertial measurement units. We use the reported RPE values of each player to train a machine learning model based on the engineered features in a supervised learning task (LeCun et al., 2015). The engineered features and their corresponding RPE values were used to create transactions for each player and session. By combining all of these transactions, the final dataset for the experiments was formed.

Data acquisition was facilitated through the Polar Team API, which enabled the transfer of data into a local MongoDB database (version 4.4.8). Subsequent data processing and analysis were carried out using Python (version 3.10) and the Pandas library (version 1.4.4). A comprehensive set of 174 internal and external load parameters was calculated, as detailed in Table 1. Herein, we outline some parameters more prominently.

From the recorded heart rate, we derive various quantitative features, such as the mean, median, standard deviation, minimum, and maximum values. To establish heart rate zones, we utilize the individual maximum heart rate (HR_max) of each player. Each heart rate zone was defined as follows: Zone 1 = <30% HR_max, Zone 2 = 30-39% HR_max, Zone 3 = 40-49% HR_max, Zone 4 = 50-59% HR_max, Zone 5 = 60-71% HR_max, Zone 6 = 72-81% HR_max, Zone 7 = 82-87% HR_max, Zone 8 = 88-92% HR_max, Zone 9 = >92% HR_max. (Seiler, 2010).

We included statistics and other calculated features that represent the absolute, percentage and periodicity values of time spent in each zone. In order to eliminate artifacts, here we define a period as a single subsequence (longer 1 sec) within a session.

The training impulse (TRIMP) was calculated as described by e.g. (Calvert et al., 1976). For TRIMPs, we calculate three versions: TRIMP (all), TRIMP (>4), and TRIMP (<5): The heart frequency zones from 1-9 described above were used to calculate the three TRIMPs. In order to better distinguish the influence of lower and higher zones, TRIMP (<5) is limited to the heart frequency zones smaller than 5 and TRIMP (>4) to the heart frequency zones larger than four. TRIMP (all) includes all heart frequency zones.

Parameters related to external load where obtained using the Polar Team Pro System as detailed above. Features related to GPS and inertial measurement units in our analysis encompass statistical measures such as mean, median, standard deviation, and interquartile range, alongside kinetic energy, count of values surpassing the mean, and the extreme values. For categorizing speed zones, we followed the classification proposed by (Gualtieri et al., 2023) which specifies: Zone 1 as 0-9 km/h (sustained for 5 seconds), Zone 2 as 10-13 km/h (5 seconds), Zone 3 as 14-19 km/h (5 seconds), Zone 4 as 20-24 km/h (2 seconds), and Zone 5 as 25 km/h or more (1 second). Subsequently, different features were computed for each training session (Table 1).

In addition, we incorporated a comprehensive set of features to capture covered distance and duration during high-intensity running (HIR) defined as velocities exceeding 14.4 km/h according to the definition provided by Coutts et al. (2010). We integrated session-based metrics encompassing total distance covered, speed and distance, as well as duration. In line with the existing body of research, we included PlayerLoad™ as an additional external load indicator (Barrett et al., 2014). PlayerLoad^TM is described in arbitrary units derived from three-dimensional measures of the instantaneous rate of change of acceleration measeured by tri-axial accelerometers (Barrett et al., 2014). The utility of PlayerLoad^TM as an indicator of training load has been validated against benchmark measures of both external load (such as distances covered) and internal load (including heart rate and ratings of perceived exertion) in training environments (Barrett et al., 2014).

For predicting RPE using our engineered features, we utilized ordinal regression across various machine learning models, as detailed in Table 2. The set of machine learning models was selected to cover a wide range of approaches in the field of machine learning: Linear regression with regularization is a simple application that is well suited to identify linear relationships in the data. K-nearest Neighbor offers good performance on small datasets and tree-based approaches are well suited to model non-linear characteristics in the data (Müller and Guido, 2016).

All machine learning models were adapted from the Scikit-learn library (v1.1.2, https://scikit-learn.org).

Our training methodology for the machine learning models starts with splitting our dataset into two subsets: training and test sets. To enhance the robustness of our evaluation, we employed n-fold cross-validation. This technique iteratively partitions the dataset n times, varying the test set composition in each iteration to ensure every data point is included exactly once in the test set. This strategic procedure ensured the independence of results from the test dataset split. Specifically, we opted for a 5-fold cross-validation to ensure a sizable and representative test group for our analysis.

The training dataset formed the basis for training the machine learning model, with the anticipated RPE serving as the target in a supervised learning framework. To enhance our model's performance, we implemented a randomized grid-search approach for optimal machine learning model configuration (Bergstra and Bengio, 2012). This process involved systematically varying hyper parameter combinations within a predefined range to find the most effective set for our specific task. Each model underwent rigorous training with all dataset splits and across diverse hyper parameter configurations. After this extensive training, the models were evaluated using the test dataset from the current cross-validation split, comprising data not used in training, to ensure an unbiased evaluation of the model's efficacy.

Figure 1 illustrates our self-designed deep learning artificial neural network regression model.

The training and evaluation of the ANN closely mirrored the machine learning process described before. As an additional step in the ANN training process, the training dataset was further partitioned into a training dataset (80%) and a validation dataset (20%).

In the training phase of the ANN, the model's performance was evaluated at each epoch using the validation dataset. The goal was to pinpoint the epoch where the ANN demonstrated peak performance. This involved tracking various performance metrics to confirm the model's effective learning from the training dataset, while avoiding overfitting. Overfitting occurs when a model becomes overly specialized to the training data, compromising its generalizability to new, unseen data.

By scrutinizing the performance on the validation dataset across epochs, we pinpointed the epoch with the optimal model performance and made informed decisions regarding the model's generalization capabilities. This careful validation process was essential for ensuring the NN's robustness and its ability to make accurate predictions beyond the training dataset (Ripley, 2007). The resulting model is then tested with the heldout test dataset to evaluate its performance on unseen data. The metrics on the test dataset determine the final outcome of the model.

The deep learning model composed of multiple fully connected feed-forward layers, activation functions and residual connections (Chollet, 2021). Its architectural structure was elucidated as follows:

Input stack: This initial component of the network served to transform the input dimension into a higher dimension denoted as "d_encode." It achieved this through a sequence of two feed-forward layers;

Middle blocks: The central portion of the network comprises N identical blocks. Each of these blocks encompasses two feed-forward layers, each of which is enveloped by a sigmoid activation function, and a dropout layer is interposed between them. These blocks also feature a pivotal component where the output is augmented with a residual connection from the inception of the block. Additionally, layer normalization, as outlined by Lei Ba et al. (2016), was applied within each block;

Last layers: The concluding segment of the model consists of three feed-forward layers that further transform the dimensionality from "d_encode" into the final output of the model.

The optimization process was conducted using the Adam optimizer, as detailed by Kingma and Ba (Kingma and Ba, 2014) and employed a batch size denoted as "n_batch." Throughout our experiments, we systematically tuned the hyperparameters, including "d_encode", "N", "n_batch", and the learning rate, utilizing a grid search methodology. This rigorous parameter optimization enabled us to identify the most suitable deep learning model configuration that aligns with the specific requirements of our use case.

To ensure consistent training of the machine learning and deep learning models, we applied min-max normalization to each feature, scaling them between 0 and 1. The dataset was shuffled using a fixed seed to maintain reproducibility. We trained all models using 5-fold cross-validation, securing test split independence in our results. The reported scores represent the mean and standard deviation across all cross-validation splits. To balance the distribution of RPE target values, we performed oversampling for each dataset split, utilizing the Synthetic Minority Over-sampling Technique (SMOTE) (Lemaitre et al., 2017).

To ensure an equal distribution of the RPE values during model training, oversampling of the dataset was performed. The distribution of the RPE values in the raw dataset is highly unbalanced (Figure 2). RPE values with a higher appearance would cause a bias in the prediction model, which would limit the general validity of the model.

Our detailed data analysis revealed an uneven distribution of RPE values throughout the dataset, both in the complete dataset and in a subset excluding games. To address this imbalance, we divided our experiments into two separate datasets: one inclusive of all data and the other excluding games. This division enabled us to perform tailored evaluations for each dataset, aligning our analysis with the specific conditions of each dataset.

For the dataset including games, we introduced an innovative feature to quantify each player's total playtime. This feature accurately accounts for player substitutions during games and factors in red card occurrences, ensuring a precise estimation of playtime for every player.

For the training process, well-established error measures for regression tasks were employed. The set ŷ ∈ Ŷ contains the classification values, and the set y ∈ Y represents the actual measured values.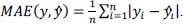

n represents the size of the samples, which is equal in both datasets. The mean absolute error (MAE) describes the error between paired observations and is defined as follows:

The MAE had the same scale as the measured data and is used for evaluation. We choose MAE as it is robust against outliers and offers intuitive interpretationt. Similar to the MAE, the mean squared error (MSE) describes the errors between paired observations; however, due to the squared function, the MSE penalizes outliers more than smaller errors, thus allows to measure the models’s robustness against outliers.

To calculate the loss, the MSE was computed as follows: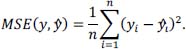

The mean absolute percentage error (MAPE) is an error measure indicating the deviation from the classification to the actual measured value. The deviation is expressed as a percentage and is therefore dimensionless, allowing better comparabillity to other datasets.

We use the MAPE for the final evaluation, which is defined as follows: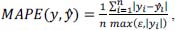

where ε represents an arbitrary small positive number to prevent undefined results when y_i is zero.

To streamline our model and ensure its stability (Hansen and Yu, 2001; Kuhn and Johnson, 2019), we performed a feature reduction process by conducting a correlation analysis employing the Pearson correlation coefficient. When the absolute correlation coefficient between two features exceeded 0.9, we removed one of these redundant features. This led to the removal of 64 features, resulting in a final dataset of 108 features.

To ensure comprehensive evaluation and ascertain the robustness of our model, experimental analyses were carried out on two datasets: one with reduced features and another containing all features without exclusions.

To assess the comparability of our dataset with related work, we calculate the Pearson Correlation of our characteristics with the target value (RPE). This makes it possible to estimate the information value of the features in relation to the target variable (RPE) and thus to estimate the modeling effort of the machine learning model and the deep learning model. In our final dataset, that will serve as input for the machine learning a deep learning models, we discovered heart rate zone 8 and 7 related features to result in the highest correlation with a Pearson Correlation of 0.161 (see Table 3 for top ten correlations). Bartlett et al. (2016) reported a considerable higher Pearson Correlation of 0.77 with session distance and 0.69 with high speed running. Accordingly, it is substantially more difficult to determine RPE values in our data set compared to the data set from Bartlett et al. (2016).

The outcomes of all machine learning models, including their respective best hyper parameter combinations, are displayed in Table 4. The reported scores represent the mean performance on the test sets obtained through 5-fold cross-validation.

Both machine learning and deep learning models exhibited superior performance on the dataset when excluding the data from soccer matches. Our self-designed deep learning architecture demonstrated notably enhanced results on the dataset without games. The deep learning model performed better when all features were included, whereas machine learning models showed improved performance with reduced features.

Feature importance analyses revealed a mean/median feature importance of 0.58/0.59 (±0.19) in our dataset without exclusion (174 features) and 0.93/0.92 (±0.25) in our reduced dataset (108 features), whereas maximum heart rate was the most important feature with a relative importance of 1.81% for the top ten important features for both datasets (Figure 3 and Figure 4).

For the deep learning model, a hyperparameter study with a grid search in the following parameter ranges was performed: d_encode: [1024, 2048, 4096], N: [5, 10, 20, 25, 35, 50, 60, 70], n_batch: [4, 8, 16], and the learning rate: [10e-3, 10e-4, 10e-5]. An early stopping with a patience of 15 epochs and a minimum change threshold in the MAE metric of 0.05 for the model training was employed. The best hyperparameter constellation was d_encode = 4096, N = 10, n_batch = 4, learning rate = 10e-5 resulting in a MAE of 1.04 (±0.07). The final model contains 353M trainable parameters.

This article aimed to identify which external and internal load parameters correlate with subjective RPE, assess various machine learning models for estimating RPE, and to develop a deep learning architecture for predicting RPE based on objectively measured external and internal load parameters. The main results of our study are that a multitude of objectively assessed external and internal parameters affect RPE (most prominent ones being maximum heart rate, maximum acceleration, and total distance covered in speed zone 10-13 km/h), and that out of the herein investigated machine learning models, the ExtraTree machine learning model outperforms other machine learning models when predicting RPE with a Mean Absolute Error (MAE) of 1.25 (±0.01). Additionally, our designed deep learning architecture performed best with a Mean Absolute Error (MAE) of 1.04 (±0.07) RPE units. The ExtraTree model achieved comparable results on the MSE/RMSE metric (ExtraTree RMSE: 1.63 (±0.04), deep learning RMSE: 1.64 (±0.05)). We found that the results with the dataset that included games were slightly lower compared to the dataset where games were removed. With data from games, we noticed different values than in training sessions, especially for the data related to internal load. We suspect that the total number of games in the dataset was too small for our models to be able to model these deviations.

Our research contributes to existing literature by expanding upon prior studies (e.g (Bartlett et al., 2016; Vallance et al., 2023; Jaspers et al., 2018) that utilized machine learning or artificial neural networks to predict RPE based on objective measures. Unlike previous studies (Bartlett et al., 2016; Vallance et al., 2023; Jaspers et al., 2018), our analysis was based on a broader range of input data and features generated from it and was limited to a purely data-centric approach.. This has the advantage of being independently applicable to other athletes and having no dependencies on specific values, such as RPE of an athlete from the past (Jaspers et al., 2018).

Our research, involving 174 input parameters, demonstrated that RPE cannot be predicted by a single variable; instead, a combination of multiple parameters is necessary. Among the parameters analyzed, maximum heart rate emerged as the most significant predictor of RPE, followed by maximum acceleration, the distance covered within the 10-13 km/h speed zones, the absolute count in heart rate zone 7, and the time spent in the high-speed zone (exceeding 14.4 km/h).

In our study, we explored different machine learning methods to predict RPE using a combination of internal and external load data. The outcomes for the machine learning models revealed that tree-based models achieved the lowest error in predicting RPE, with a MAE of 1.25 (±0.01). It is likely that this improved performance is largely due to the feature boosting process used in tree-based models such as ExtraTree, which enables the extraction of feature details that are critical to the corresponding prediction. In feature boosting, the model adds trees sequentially, with each new tree trained to correct the errors of the ensemble of previous trees, improving the overall accuracy of the model (Geurts et al., 2006).

Compared to machine learning models, our self-designed deep learning architecture exhibited smaller MAE. However, the ExtraTree machine learning model showed comparable MSE and RMSE to the deep learning architecture (ExtraTree RMSE: 1.63 (±0.04) vs. DL RMSE: 1.64 (±0.05)). When converting the error assessment outcomes from the machine learning and deep learning models into practical insights, our deep learning model seems to be more suitable for more homogeneous athletic groups with fewer outliers. On the other hand, in scenarios involving more heterogeneous athletic groups, which typically include more outliers, the ExtraTree model emerges as the more appropriate choice. Future research should explore the efficacy of the deep learning model proposed in this study using data from a broader spectrum of athletes. This is particularly important because deep learning models generally show improved performance when trained with larger datasets (Goodfellow et al., 2016).

We were unable to reproduce the error rates of Bartlett et al., who achieved an RMSE of 1.42 (Bartlett et al., 2016), or of Vandewiele et al., who reported an RMSE of 0.85 in a comparable RPE prediction task (Vandewiele et al., 2017). Although it's speculative, the smaller error rates observed in the study by Vandewiele et al. might be attributed to overfitting in their stacking model, which potentially could be due to the inclusion of individual, athlete-specific characteristics, such as the athletes' names and ages, in their RPE prediction model. (Vandewiele et al., 2017). Incorporating specific details like athletes' names and ages might reduce error rates in RPE prediction models. However, this approach hinders the model's generalizability to different athlete cohorts, thereby limiting its practical applicability in broader contexts. In the case of Bartlett et al. (2016), the smaller error rates could stem from high correlations between the input parameters that have been used to train the developed models and RPE. Our dataset exhibited low correlation between the input parameters used for training our machine learning and deep learning architectures and RPE. Additionally, the work of Vandewiele et al. (2017) or Bartlett et al. (2016) did not report important preprocessing steps such as over-/under-sampling (Goodfellow et al., 2016) to mitigate unequal distribution of collected RPE data to prevent bias in the model training process. Given these differences, it appears impractical to compare the performance of our machine learning models and deep learning architecture with the works of (Bartlett et al., 2016; Vandewiele et al., 2017).

Athletes and coaches in the domain of soccer may utilize the in this study developed algorithms and trained models to predict RPE with a MAE of 1.15 ± 0.03. This prediction is valuable if the athlete-reported RPE is missing due to low compliance or for comparing the reported RPE with the predicted RPE. Such a comparison is beneficial for identifying discrepancies that might indicate increased athlete fatigue (if the athlete-reported RPE is higher than the predicted RPE) or improved athlete "fitness" (if the athlete-reported RPE is lower than the predicted RPE). Additionaly, coaches might use our algorithms to plan training more precisely in order to avoud differences between planned RPE values by coaches and perceived RPE by athletes (Inoue et al., 2022).

Our study's strength lies in the meticulous preprocessing of data to eliminate bias in the model training process. This was achieved by over-/undersampling RPE values to ensure an even distribution within the dataset. Furthermore, all models in our study were trained using 5-fold cross-validation, guaranteeing that our reported results are independent of the test dataset.

We conducted a thorough evaluation of nine machine learning architectures and a self-designed deep learning architecture, adhering to state-of-the-art concepts for RPE prediction, which bolsters the credibility of our findings.

However, our study is limited by its focus on a small cohort of professional soccer players. Future research should encompass a larger pool of soccer players and athletes of other sport domains to enhance the training, potentially improving the performance of machine learning and deep learning models and to further promote generalization and transferability into practice.

The broad spectrum of deep learning offers many regression-focused architectures detailed in existing literature. Future studies should assess and compare these various models with our custom-designed approach. Additionally, future research should incorporate other parameters not explored in this study, such as previously reported RPE, using the machine learning and deep learning architectures developed herein.

Our main conclusion is that a multitude of external and internal parameters influence RPE prediction in professional soccer players. Out of the 174 investigated parameters, maximum heart rate during training or competition has the strongest influence on RPE.

We revealed that the ExtraTree machine learning model, compared to the other investigated machine learning models, achieves the lowest error rates (MAE: 1.15 (±0.03)), is applicable to players beyond those included in this study, and can be executed on almost any currently available laptop. The herein developed state-of-the-art neural network exhibits small error rates (MAE: 1.04 (±0.07)), but due to the high computing power needed, the ExtraTree machine learning model seems to be more suitable in practice.