|
|
|
| |
| ABSTRACT |
|
This study suggests a wearable sensor technology to estimate center of mass (CoM) trajectory during a golf swing. Groups of 3, 4, and 18 participants were recruited, respectively, for the purpose of three validation studies. Study 1 examined the accuracy of the system to estimate a 3D body segment angle compared to a camera-based motion analyzer (Vicon®). Study 2 assessed the accuracy of three simplified CoM trajectory models. Finally, Study 3 assessed the accuracy of the proposed CoM model during multiple golf swings. A relatively high agreement was observed between wearable sensors and the reference (Vicon®) for angle measurement (r > 0.99, random error <1.2° (1.5%) for anterior-posterior; <0.9° (2%) for medial-lateral; and <3.6° (2.5%) for internal-external direction). The two-link model yielded a better agreement with the reference system compared to one-link model (r > 0.93 v. r = 0.52, respectively). On the same note, the proposed two-link model estimated CoM trajectory during golf swing with relatively good accuracy (r > 0.9, A-P random error <1cm (7.7%) and <2cm (10.4%) for M-L). The proposed system appears to accurately quantify the kinematics of CoM trajectory as a surrogate of dynamic postural control during an athlete’s movement and its portability, makes it feasible to fit the competitive environment without restricting surface type. |
| Key words:
Wearable technology, golf swing, center of mass, dynamic postural control, balance, simplified biomechanical model of human body
|
Key
Points
- This study demonstrates that wearable technology based on inertial sensors are accurate to estimate center of mass trajectory in complex athletic task (e.g., golf swing)
- This study suggests that two-link model of human body provides optimum tradeoff between accuracy and minimum number of sensor module for estimation of center of mass trajectory in particular during fast movements.
- Wearable technologies based on inertial sensors are viable option for assessing dynamic postural control in complex task outside of gait laboratory and constraints of cameras, surface, and base of support.
|
Postural control and functional balance play a key role in athletic performance as well as prevention of sport related injuries (Hale et al., 2007; Hume et al., 2005; Tropp et al., 1985). Many times, athletic trainers attempt to improve the balance or handle a weight shift during performance (Sell et al., 2007) of their athletes in order to enhance performance, prevent injury, or recover after injury (e.g., ankle sprain) (Wikstrom et al., 2010). It is known that low handicap golfers have better balance abilities (Sell et al., 2007). Therefore, an accurate quantification of an athlete’s dynamic balance control in the field may play an important role in many sport applications. Due to measurement ease, postural control is often assessed by measuring center of pressure (CoP) sway or its trajectory using a force platform (Najafi et al., 2012). However, standing on an instrumented platform makes it difficult to examine postural control on different surface types which better replicate an athlete’s natural competitive environment. Recently, several wearable technologies have been developed to evaluate body motion (e.g. body segment sway) based on microelectro-mechanical sensors (MEMS) (Adlerton et al., 2003; Allum et al., 2001a; 2001b; Allum et al., 2002, Mayagoitia et al., 2002, Najafi et al., 2002,). Key advantages of body-wearable sensors are their low cost and portable usage in many environments (Aminian et al., 2002; Najafi et al., 2003; 2009; 2010a; 2010b; Russmann et al. 2004). Body-wearable sensors often consist of one or a combination of accelerometers, angular velocity sensors, and magnetometers providing valuable data in research (Russmann et al., 2004). By attaching these sensors to a body segment, they allow measurement of segment motion or body sway while balance tasks are performed (Najafi et al., 2010a; 2012; Mancini et al. 2012). Several studies have demonstrated that sensor derived parameters from wearable technologies are useful as an objective metric for assessing postural control deterioration due to a disorder (e.g. Parkinson’s, diabetes) or aging (Mancini et al., 2011; Mancini et al., 2012; Najafi et al., 2012; Toosizadeh et al., 2014b). Wearable technologies are also sensitive enough to track changes in post–intervention postural control (Grewal et al., 2013, Toosizadeh et al., 2014a) or predicting prospective falls (Schwenk et al., 2014). Key challenges of using wearable sensors include their inability to extract useful clinical data when there is too much noise, restriction on the number of sensors that can be attached, and their ease of management. Therefore, a simplified biomechanical human body model with the minimum number of sensor attachments required should be implemented with such technology to make them suitable for clinical applications. On the other hand, model simplification may alter system accuracy, thus, an optimum tradeoff between accuracy and minimum number of sensor attachments should be provided. Previous studies addressing wearable technology for assessing postural control often focus on sacral region motion (e.g., one link) and deem to be sufficient in estimating the center of mass (CoM) sway assuming hip joint movement is limited (Allum et al., 2001a, Aramaki et al., 2001; Adlerton et al., 2003). This approach may produce accurate results during quiet standing or walking a straight line but may be inappropriate for measuring CoM trajectory during athletic movements with significant body segment motions. This study aims to explore the accuracy of wearable sensors together with simplified biomechanical models for estimating CoM trajectory during significant body segment movements. To achieve this goal, three studies were designed to explore the accuracy of main inputs of the proposed model. First, sensor accuracy for estimating 3D body segment angle was assessed. For this purpose, accuracy of the system to estimate trunk 3D angle was estimated. We assumed similar accuracy would be obtained if sensor was attached to other body segments. Second, accuracy of three simplified models to estimate CoM trajectory were evaluated and compared to the reference system. These models estimate CoM trajectory using either 1) a single sensor model attached to subject’s lower back (Model 1); 2) two sensor modules, respectively attached to subject’s lower back and shank (Model 2); or 3) three sensor modules, respectively attached to subject’s lower back, thigh, and shank (Model 3). Through this study, the optimum model, which includes minimum number of sensor module attachments and an acceptable accuracy, was selected. Finally, the accuracy of the optimum model for estimation of CoM trajectory in medial-lateral (M-L) and anterior-posterior (A-P) planes with respect to foot position were examined during a series of movements including golf swings. Experimental protocolThree studies were performed to examine different inputs of the final model. Study 1 explored the accuracy of the proposed sensors for estimating 3D body segment angle. In this study, a camera-based motion analyzer (Vicon®, Oxford, UK) was determined as the reference standard. Study 2 measured accuracy of three simplified models for estimating CoM compared to a full-body CoM estimation model using Vicon during a series of voluntary movements. Study 3 compared the output of the selected model for estimation of CoM trajectory during golf swings.
Participant recruitmentA total of 25 participants including groups of 3, 4, and 18 were recruited from the Rosalind Franklin University campus for each respective study. All studies were approved by the local Institutional Review Board at Rosalind Franklin University, North Chicago, IL, USA and participants signed an approved informed consent form prior to participation. Three healthy male participants participated in Study 1 (age: 23.3 ± 0.6 years; height: 1.80 ± 0.07 m; body mass: 70.3 ± 8.1 kg), four healthy males in Study 2 (age: 38.4 ± 17.5 years; height: 1.84 ± 0.03 cm; body mass: 84.1 ± 12.3 kg), and 18 golf players (12 males and 6 females) with an established handicap level (9-19; average handicap: 14.9 ± 3.1) were recruited (age: 38.4±12.3 years; height: 1.78 ± 0.09 cm; body mass: 80.4 ± 14.2 kg).
Equipment and reference systemDepending on the study, up to three inertial sensors, each including a triaxial accelerometer, triaxial gyroscope, and a triaxial magnometer (LEGSys™, BioSensics LLC, Boston, MA), were attached respectively, to subject’s shin, thigh, and lower back using comfortable Velcro bands as shown in Figure 3. The sensors provided real-time kinematic data (sample frequency 60Hz) including acceleration and speed of rotation as well as quaternion (qw, qx, qy, qz) components (Dumas et al., 2004; Hart et al., 1994; Kingston and Beard, 2004) that were subsequently converted to Euler angles (Najafi et al., 2010a). These angles were used to describe a sequence of three rotations determining the orientation of a rigid body in three dimensions, in their order of application are: i) Yaw (t, M–L), ii) Pitch (L, A–P) and iii) Roll (P, I–E). The resulting three-dimensional angles were used to estimate the trajectory of a participant’s segments such as shank, thigh or upper back depending on the simplified human body model. We assumed each body segment to be rigid, thus considering that the wearable sensors directly provide segment angle, our models were not sensitive to the exact location of sensor attachment. A five-camera based motion analyzer system (Vicon®) was used as the reference standard. The sample frequency of Vicon system was set to 60Hz to facilitate synchronization between inertial sensors and output of Vicon system. To synchronize between two systems, at the beginning of each measurement, subjects were asked to bend their trunk forward and back. The time of maximum trunk tilt measured by two systems via the markers and sensors attached to the lower back was used to synchronize between two systems as illustrated in Figure 5. For all experiments, the anterior-posterior (A-P) direction was defined as the rotation in the sagittal plane, rotation in the frontal plane characterized as medial-lateral (M-L) direction, and the internal-external (I-E) was assumed as rotation in the transversal plane, all in respect to the subject’s upright position. To explore the degree of agreement between range of CoM sway estimated by each model and the range of center of pressure (CoP) sway, measured by a standard pressure platform, subjects in Study 2, were asked to perform golf swing trials while standing on a pressure platform (Emed® System, Novel, Germany, Figure 2). This may limit the base of support favored by golfers. Thus, after selection of the optimum model, further evaluation was performed without a pressure platform (Study 3, Figure 3), and participants were allowed to self-select their base of support prior to each swing.
Protocol of measurement
Study 1: Estimation of a typical 3D body segment angle (lower back angle)To reduce the impact of potential artifact due to movement of skin for the reference system, all Vicon markers and inertial sensor were placed on a rigid plate attached to the participant’s lower back between the 10th thoracic vertebra (t10) and 5th lumbar vertebra (Figure 1). The reference trunk tilt was calculated from the 3-D components of the markers in each direction as described in our previous publication (Najafi et al., 2002). Before each test, the A-P direction of the participant was visually aligned to the Vicon’s y-axis origin. Using the coordinates extracted from the markers, the projection of lower back angles along each axis were estimated. Participants executed a series of voluntary movements while standing, including bending forward and backward (A-P), bending side-to-side (M-L) and rotating right to left (I-E). Participants were asked to repeat each test at a self-selected pace including slow, normal, and as fast as he/she could. Data from the sensors and Vicon were synchronized by matching the identified positive peak (i.e. maximum tilt angle) of the measured angle by each system.
Study 2: Estimation of center of mass using simplified modelsA set of 36 reflective markers were positioned on the participant to estimate CoM as suggested by Vicon’s "Plug-in Gait full body modeling" along with a single sacral marker (Najafi et al., 2012). The model measures the CoM of 47 segments including each hand, femur, tibia, foot, humerus, radius, thorax, pelvis, and head. For estimation of anthropometry data, the toolbox uses height, weight, leg length, knee width, ankle width, shoulder offset, elbow width, wrist width, and hand thickness. This model provides an automatic generation of the CoM 3D position after reconstruction for all body segments (Figure 2). Each participant performed three golf swings as well as a series of voluntary movements as described in Study 1. The CoM during each swing was estimated using different simplified models explained below. The estimated values were then compared with the estimated value using the full body model discussed above.
Study 3: Estimation of center of mass using wearable sensorsA set of 5 reflective markers were positioned on specific anatomical landmarks of the participant: 7th cervical vertebra (c7), 10th thoracic vertebra (t10), flexion-extension axis of the knee, lower lateral surface of the thigh, and shank (Figure 3). Along with the reflective markers, three wearable sensors were attached to the participant. One sensor was attached on the upper back between c7 and t10 using a body strap, one to the shank using a shin brace and one to the thigh using an elastic strap (Figure 3). Subjects were asked to hit a reflective ball with a common driver club. Initially, the subject was instructed to stay in a neutral upright position to synchronize the position of the markers and the sensors as the zero spot and then to bend (A-P direction) and return to the initial position. The peak of this movement was detected to synchronize the two systems before each swing. After three swings were performed, data collected was reconstructed using Vicon Nexus software for comparison between Vicon and the sensors (ver 1.4). To estimate CoM, we used the optimum model identified in Study 2. The output of the data using the Vicon model was then set as the reference standard to evaluate the accuracy of the sensor data model.
Models: Estimation of center of mass using body worn sensorsTo estimate the CoM position, we assumed the body, during standing, can be modeled by a one, two or three-link model. One-link model: The one-link model simulated a single inverted pendulum model with motion around the ankle joint (Figure 4a), assuming hip and knee motion is limited compared to ankle motion. As suggested by previous literature, CoM can be estimated from the motion of the lower back (i.e. sacrum) (Adlerton et al., 2003, Moe-Nilssen and Helbostad, 2004). The motion of the sacrum during upright position measured with the Vicon system was used to evaluate the validity of this assumption. Assuming this model, projection of the sacrum motion allows estimation of the ankle’s angle in respect to natural position in A-P (θ¸a) and M-L (φa) directions. The CoM position can then be estimated using the following formula:
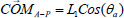 |
(1) |
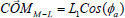 |
(2) |
Where L1 represents the distance between sacrum and foot estimated using Vicon data. Two-link model: Figure 4b illustrates a two-link model to estimate the CoM trajectory using the information from joint angles and the participant’s anthropometric data. In this model, knee joint motion was assumed to be negligible compared to ankle and hip motions. Although, the model allows estimating 3D CoM motion, in this study, we only estimated the CoM trajectory in M-L and A-P directions. For all estimations, the joint angles and CoM value were assumed to be zero at neutral position, when participant was at rest in an upright standing posture. The sensors attached to participant’s trunk and shank provided respective angles during neutral position. It was assumed that subtracting trunk and shank angles would provide the hip joint angle (θ¸h, Figure 4b). On the same note, ankle joint angle in respect to neutral position (θ¸a) was assumed to be equivalent as the estimated shank angle. Having the anthropometric data of each participant (e.g., body mass m and height H), the position of each link’s CoM in the sagittal plane was described as:
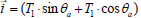 |
(3) |
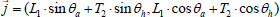 |
(4) |
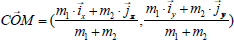 |
(5) |
Here, θ¸a, and θ¸h represent, respectively, the angular displacement of the ankle and hip in neutral position (Figure 4b). The first component of the CoM (x values) corresponds to the movement in A-P direction, expressed as:
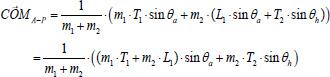 |
(6) |
The equations can be rewritten with two constants:
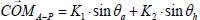 |
(7) |
Where
The equation of the CoM in the M-L direction was derived in an analogous fashion using the estimated angles in M-L plan (φ angle). The values of m1 and m2 (distal and proximal mass segments), T1 and T2 (distal and proximal CoM segments), and L1 and L2 (distal and proximal length segments) were estimated using the participant’s body mass and height as explained by Winter et al.(Winter 1990). To reduce noise and artifact such as skin movement, the angle data was filtered using wavelet transform band pass filter with mother wavelet of ‘Coiflet 5’ and cut off frequency 0.06-30Hz as suggested in our previous studies (Aminian et al., 2002, Najafi et al., 2002; 2003). Three-link model: For the three-link model (Figure 4c), the proximal segment was divided in two sections (shank and thigh) which accounts for the bending of the knees (θ¸k). Similar to the approach explained in the two-link model, the CoM equation based on a three-link model can be rewritten as follows:
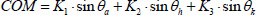 |
(8) |
Where
Statistical analysisAgreement between estimated body segment angle (i.e. lower back angle) by inertial sensors and reference system was evaluated using Pearson correlation coefficient (r-value). Where point-to-point agreement between two systems was estimated per subject for each measured CoM trajectory as a function of time, the average and standard deviation of all estimated r-values were reported. Additionally, the systematic (SE), random (RE) and root mean square error (RMSE) of the angles between the two systems were calculated for each trial. Systematic and random errors were estimated, respectively, by calculating mean and standard deviation of errors. The accuracy of each model for estimating CoM was assessed by examining the degree of agreement between each model and the reference standard (Vicon). The degree of agreement was estimated using Pearson correlation coefficient. The SE, RE, and RMSE were also calculated for the CoM range of motion. To evaluate the discrepancy of measurement between sensor-derived and Vicon-derived parameters, Bland-Altman plot was used. To explore whether the proposed model and algorithms allow real-time estimation of body segment angle and CoM trajectory, using the Matlab timer (Tic-Toc function), we controlled the execution of each trial for estimating and recording 3D angles of two segments calculating CoM trajectory. We assumed that the algorithm could be implemented in real-time if the time required for estimation of each time sample is less than 0.0167sec corresponding to sample frequency of 60Hz used in our study. All calculations and statistical analysis were made using MATLAB® version 7.4 (R2007z) (MathWorks, Inc., Natick, MA).
Accuracy of body worn sensors for estimation of joint anglesA relatively high agreement was observed between the sensor’s output and the reference system for both spontaneous angles and range of motion values (r > 0.99, p < 0.001). Figure 5 illustrates the estimated angles using Vicon (dash line) and inertial sensors (solid line) for a typical participant during sagittal plane movements. Table 1 represents the averaged values for point-to-point estimated angles including SE, RE, and RMSE errors extracted for the fast, medium, and slow speed movements. Random errors in the A-P direction were less than other directions and reached to less than 2.2% (<1.72°), 1.47% (<1.20°), and 0.99% (<0.78°) for the fast, medium and slow speed movements, respectively. The random errors in other directions were also relatively low and reached to maximum value of 3.43% (5.48°) in I-E direction during fast movements. On the same note, the errors for range of motion were relatively low (Table 2). For example, the random errors in A-P direction was on average 4.8% (3.7°), 3.8% (3.1°), and 2.6% (2.1°) respectively for the fast, medium, and slow speed movement trials. Similar errors were observed in other directions.
Accuracy of CoM estimation using single link or multiple-link modelsA moderate agreement was observed between the CoM estimation using the one-link model compared to the reference system. The correlation coefficient between estimated CoM using one-link model and reference system was r = 0.52 ± 0.41 for A-P and r = 0.52 ± 0.49 for M-L direction. However, the correlation between the CoM estimation using a two-link model and the reference system was high (intra-subject point-to-point correlation: r = 0.93 ± 0.05 for A-P and r = 0.95 ± 0.03 for M-L directions). On the same note, the errors of CoM estimation using two-link model were relatively low (Table 3). Specifically, the average random error was 2.46cm (11.18%) and 3.88cm (14.64%) respectively for the CoM range of motion in A-P and M-L directions. The three-link model also produced high agreement with the reference system. The observed intra-subject point-to-point correlation coefficient was r = 0.94 ± 0.05 for A-P and r = 0.91 ± 0.03 for M-L directions. In A-P direction, the random errors average was 2.05cm (9.3%) and 1.1cm (5%) for systematic errors (Table 3). Surprisingly, the error was slightly higher than two-link model for M-L direction (5.3cm (19.96%) three-link model vs. 3.88cm (14.64%) two-link model). On the same note, a relatively high agreement was observed while comparing the CoM range estimated using 2- and 3-link models as well as COP range estimated using pressure platform when CoM range was estimated using Vicon system in both AP and ML directions (Figure 6).
Accuracy of CoM estimation for athletic movements (i.e. Golf Swing)In Study 3, we examined the accuracy of the two-link model for estimation of CoM which relatively offered the best combination of the required minimum number of sensors with maximum accuracy. Results suggest a relatively high agreement between the estimated CoM and reference system for golf swing trials particularly in the A-P direction. The correlation coefficient for estimated CoM range of motion was r = 0.91 ± 0.05 and r = 0.71 ± 0.20 respectively for A-P and M-L directions. During golf swing trials, the average CoM range of motion was 12.96cm (A-P) and 19.35cm (M-L). CoM range of motion was calibrated using data gathered from Study 2. After calibration, the point-to-point errors for estimation of CoM were relatively low considering the small CoM range of motion (Table 4). Specifically the average random error was less than 1cm (7.7%) for A-P and less than 2cm (10.35%) in the M-L direction. After calibration, a relatively high agreement (r = 0.86) was also observed between sensor- and Vicon-derived estimation for maximum distance of CoM range during each swing (Figure 7A). On the same note, Bland-Altman plot suggests low discrepancy between two measures (Figure 7B).
In this study, we suggest an innovative, portable, and cost-effective wearable sensor technology to measure CoM trajectory while standing performing simple tasks (e.g., leaning forward, backward, and side-to-side) and carrying out athletic movements (i.e. golf swing). The proposed system allows estimation of 3D body segment angles in real-time with relatively low errors in the A-P and M-L directions. The random error of approximately 2 degrees compares favorably with other reported values using MEMS technology on the knee (Favre et al., 2006; 2008) or arm motions (Luinge and Veltink, 2005; Luinge et al., 2007) where precision of less than 4° was reported. Part of our estimation errors could be due to the fact that we manually synchronized both systems. Additionally, the A-P direction of the participant was visually aligned to the Y-axis of the Vicon origin to compare the movements in all directions, which in turn may increase the error of estimation. Furthermore, discrepancies can also be accounted for the experimental protocol, the marker setup, and skin movement. Despite these limitations, the estimated accuracy was relatively high and appeared to be enough for estimation of CoM trajectory. This study also explored the accuracy of different simplified models for estimating the trajectory of CoM (point-to-point CoM displacement as a function of time). We demonstrated that using estimation of lower back motion does not precisely represent CoM motion particularly during athletic and fast movements. On the other hand, increasing the number of segments (e.g., after including thigh segment) in human body modeling does not necessarily increase the accuracy of CoM estimation especially in the M-L direction. The reduction of accuracy by including thigh segment could be explained by known noise/artifacts generated by skin movement. Movements of shank and lower back are less influenced by skin movement because of less body fat in these segments. One of the key advantages of the proposed approach is its capability of real-time execution. Using the Matlab timer (Tic-Toc function), we controlled the execution of each trial for estimating and recording 3D angles of two segments, calculating CoM trajectory, and displaying the results all within the duration of 0.0167±0.0008 seconds which is equivalent to 60Hz sampling rate. Real time estimation of CoM is of key importance for virtual reality applications as well as motor learning paradigms in which the position of CoM or joint angle should be displayed in real-time for examining or training motor skills (Najafi et al., 2012). The suggested technology allows measuring CoM trajectory as an indicator of dynamic balance control. There are many potential advantages to using this approach. Measuring CoM over CoP may increase responsiveness. Previous authors have described a high correlation (r = 0.92) between CoP and CoM with the CoM having up to 10-12 fold increased movement during balance tasks (Najafi et al., 2010). The CoP trajectory is limited to the base of support (e.g., area between the feet), whereas the CoM boundary is only constrained by the participant’s range of motion while maintaining stability. Measuring the CoP often requires a gait laboratory with dedicated platform making it difficult for infield measurement. In a subsequent study, we have demonstrated that CoM measurement is also sensitive (p < 0.05) to separate postural control strategy during golf swing between advanced (CoM area of sway: 2.25 ± 1.96 cm2), intermediate (CoM area of sway: 5.27 ± 3.81 cm2) and novice (CoM area of sway: 8.34 ± 5.77cm2) golf players (Wrobel et al., 2012). The measureable surface area of the force platform could also be a serious limitation for many athletic movements. Standing on an instrumented platform makes it difficult to examine postural control on different surface types and does not appropriately replicate an athlete’s natural competitive environment. On the other hand, camera motion analysis systems permit accurate assessment of postural control by measuring CoM sway independent of the surface type. However, wearing numerous body markers for kinematic analysis has a negative impact on swing performance (Kenny and Anderson, 2010). Furthermore, the spatial and time constraints of using a dedicated gait lab often preclude motion analysis system usage in the athletic environment or clinical setting. A future validity study, comparing athlete’s performance with and without wearing the applied sensors have to prove the assumed minimized effect on the movement pattern of the athlete. Test designs executed in a gait laboratory are generally well-controlled and often have a high reliability (Riley et al., 2008). However, unlike laboratory settings with a force platform or camera motion analysis system, wearable sensors allow field studies mirroring real-live situations in the training and competition environment. The live measurement of balance by measuring CoM during standardized situations in team sports, such as free shots in basketball then becomes possible. In addition, the used method allows the trainer to provide real-time visual feedback to the athletes concerning their CoM sway. Past research has shown that this method has improved gait stability (Bechly et al., 2013). A key challenge for using wearable sensors is that, unlike camera motion analysis system or force platform that use a fixed landmark reference (i.e. room reference axis), the axis of the sensor is highly dependent on how it is attached to the body. Therefore, for an accurate estimation of CoM in respect to body or room axis, a calibration process is required for sensor alignment. In this study, we visually aligned the sensor axis with Vicon axis and then used quaternion approach to calibrate the orientation of sensors attached to the body (Najafi et al., 2010). Inaccuracy of this method may contribute to errors observed in this study. Other factors contributing to the error of sensor-derived parameters and the proposed models include artifacts due to sensor/marker attachment and skin/strap movement and using simplified human body model instead of full human body model for CoM estimation. Limitations to this study include sample size and marker setup. The sample size for Study 1 and Study 2 may not be large enough to characterize the errors due to the sensors and the model. Furthermore, the marker setup and full body model used for estimation of CoM motion may not meet the threshold for accuracy. For Study 1, in order to reduce the inaccuracy of the reference system for estimating a rigid body segment, where angle was estimated via marker displacements, Vicon’s reflective markers and inertial sensor were placed on a rigid platform attached to the subject’s lower back. Although this setup allows fair comparison between two systems for estimating a rigid segment angle, it may not represent the natural movement of a body segment. Additionally, the setup used in the Study 1 may mask potential artifacts from skin movement which may impact the accuracy of the measurements in Study 2 and 3, where the sensors and markers were directly attached to the body using elastic bands. Furthermore, in Study 1, comparison between two systems for measuring body segment angles was done only for the lower back angle. Thus, the estimated errors may not be representative of the errors for other body segments used in this study including shank and thigh. Naturally, if the wearable sensor poses any hindrance to the participant’s movements due to the complexity of sensor attachments (e.g. multiple sensor units, location of sensor attachment, etc) or device management (e.g. limited battery life), its application for outdoor monitoring and routine clinical assessment becomes limited (Russmann et al., 2004). Additionally, future studies should address whether the estimated CoM trajectory is clinically meaningful to evaluate balance in patients and athletes. This study proposed a simple system based on two wearable sensor modules attached to subject’s shank and lower back and a simplified biomechanical human body model for estimating the center of mass trajectory with high agreement to the optical reference system (r>0.9). The proposed system overcomes the shortcomings of laboratory based measuring systems by using relatively inexpensive miniaturized MEMS technology for balance assessment in free condition independent of surface type or testing environment. This finding may open new avenues for assessing and improving postural control in patients as well as in athletes by designing novel paradigms which were not feasible in the past due to the limitation of previous technologies.
| ACKNOWLEDGEMENTS |
The authors thank Mr. Samuel Marclay, a master student visiting fellow from Ecole Polytechnique Federale de Lausanne, who contributed to this study as part of his master project. This study was supported in part by Award Number NPRP 5-086-2-031 from the Qatar National Research Foundation. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Qatar National Research Foundation. The experiment conducted fully complies with the current laws of the country in which they were performed. The authors declare no conflict of interest. |
|
| AUTHOR BIOGRAPHY |
|
 |
Bijan Najafi |
| Employment: Associate Professor of Surgery and Director of interdisciplinary Consortium on Advanced Motion Performance, University of Arizona College of Medicine, Tucson, AZ, USA |
| Degree: PhD, MSc |
| Research interests: Biomechanics of human motion, wearable sensors and biosignal processing |
| E-mail: najafi.bijan@gmail.com |
| |
 |
Jacqueline Lee-Eng |
| Employment: Research Associate, University of Arizona College of Medicine, Tucson, AZ, USA |
| Degree: BSc |
| Research interests: Wearable sensors, exercise science, and clinical research in diabetes |
| E-mail: jleeeng@surgery.arizona.edu |
| |
 |
James S. Wrobel |
| Employment: Associate Professor, Department of Internal Medicine, Division of Metabolism, Endocrinology, and Diabetes, University of Michigan, Ann Arbor, MI, USA |
| Degree: DPM, MSc |
| Research interests: Biomechanics of the foot and ankle; health services and clinical research in the diabetic foot |
| E-mail: jswrobel@med.umich.edu |
| |
 |
Ruben Goebel |
| Employment: Associate Professor, College of Arts and Science, Sport Science Program, Qatar University, Doha, Qatar |
| Degree: PhD |
| Research interests: Training-scientific application of injury prevention, risk evaluation of sports injuries, non-communicable diseases in Qatar |
| E-mail: ruben.goebel@qu.edu.qa |
| |
|
| |
| REFERENCES |
 Adlerton A.K., Moritz U., Moe-Nilssen R. (2003) Forceplate and accelerometer measures for evaluating the effect of muscle fatigue on postural control during one-legged stance. Physiotherapy Research International 8, 187-199. |
 Allum J.H., Adkin A.L., Carpenter M.G., Held-Ziolkowska M., Honegger F., Pierchala K. (2001) Trunk sway measures of postural stability during clinical balance tests: effects of a unilateral vestibular deficit. Gait and Posture 14, 227-237. |
 Allum J.H., Bloem B.R., Carpenter M.G., Honegger F. (2001) Differential diagnosis of proprioceptive and vestibular deficits using dynamic support-surface posturography. Gait and Posture 14, 217-226. |
 Allum J.H., Carpenter M.G., Honegger F., Adkin A.L., Bloem B.R. (2002) Age-dependent variations in the directional sensitivity of balance corrections and compensatory arm movements in man. Journal of Physiology 542, 643-663. |
 Aminian K., Najafi B. (2004) Capturing human motion using body-fixed sensors: Outdoor measurement and clinical applications. Computer Animation and Virtual Worlds 15, 79-94. |
 Aminian K., Najafi B., Bula C., Leyvraz P.F., Robert P. (2002) Spatio-temporal parameters of gait measured by an ambulatory system using miniature gyroscopes. Journal of Biomechanics 35, 689-699. |
 Aramaki Y., Nozaki D., Masani K., Sato T., Nakazawa K., Yano H. (2001) Reciprocal angular acceleration of the ankle and hip joints during quiet standing in humans. Experimental Brain Research 136, 463-473. |
 Bechly K.E., Carender W.J., Myles J.D., Sienko K.H. (2013) Determining the preferred modality for real-time biofeedback during balance training. Gait and Posture 37, 391-396. |
 Dumas R., Aissaoui R., de Guise J.A. (2004) A 3D generic inverse dynamic method using wrench notation and quaternion algebra. Computer Methodsin Biomechanicsand Biomedical Engineering 7, 159-166. |
 Favre J., Aissaoui R., Jolles B., Siegrist O., de Guise J., Aminian K. (2006) 3D joint rotation measurement using MEMs inertial sensors: Application to the knee joint. France. ISB-3D, Valenciennes. |
 Favre J., Jolles B.M., Aissaoui R., Aminian K. (2008) Ambulatory measurement of 3D knee joint angle. Journal of Biomechanics 41, 1029-1035. |
 Grewal G.S., Sayeed R., Schwenk M., Bharara M., Menzies R., Talal T.K., Najafi B. (2013) Balance rehabilitation: promoting the role of virtual reality in patients with diabetic peripheral neuropathy. Journal of the American Podiatric Medical Association 103, 498-507. |
 Hale S.A., Hertel J., Olmsted-Kramer L.C. (2007) The effect of a 4-week comprehensive rehabilitation program on postural control and lower extremity function in individuals with chronic ankle instability. Journal of Orthopaedic and Sports Physical Therapy 37, 303-311. |
 Hart J.C., Francis G.K., Kauffman L.H. (1994) Visualizing Quaternion Rotation. ACM Transactions on Graphics (TOG) 13, 256-276. |
 Hume P.A., Keogh J., Reid D. (2005) The role of biomechanics in maximising distance and accuracy of golf shots. Sports Medicine 35, 429-449. |
 Kenny I., Anderson R. (2010) ISBS-Conference Proceedings Archive. The effect of body markers on golf driving performance. |
 Kingston D.B., Beard R.W. (2004) AIAA 3rd Unmanned Unlimited Technical Conference, Workshop and exhibition. Real-Time Attitude and Position Estimation for Small UAVs Using Low-Cost Sensors. |
 Luinge H.J., Veltink P.H. (2005) Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Medical & Biological Engineering & Computing 43, 273-282. |
 Luinge H.J., Veltink P.H., Baten C.T. (2007) Ambulatory measurement of arm orientation. Journal of Biomechanics 40, 78-85. |
 Mancini M., Horak F.B., Zampieri C., Carlson-Kuhta P., Nutt J. G., Chiari L. (2011) Trunk accelerometry reveals postural instability in untreated Parkinson's disease. Parkinsonism and Related Disorders 17, 557-562. |
 Mancini M., Salarian A., Carlson-Kuhta P., Zampieri C., King L., Chiari L., Horak F. B. (2012) ISway: a sensitive, valid and reliable measure of postural control. Journal of Neuroengineering and Rehabilitation 9, 59-. |
 Mayagoitia R.E., Lotters J.C., Veltink P.H., Hermens H. (2002) Standing balance evaluation using a triaxial accelerometer. Gait and Posture 16, 55-59. |
 Moe-Nilssen R., Helbostad J. L. (2004) Estimation of gait cycle characteristics by trunk accelerometry. Journal of Biomechanics 37, 121-126. |
 Najafi B., Aminian K., Loew F., Blanc Y., Robert P. (2002) Measurement of stand-sit and sit-stand transitions using a miniature gyroscope and its application in fall risk evaluation in the elderly. IEEE Transactions on Biomedical Engineering 49, 843-851. |
 Najafi B., Aminian K., Paraschiv-Ionescu A., Loew F., Bula C.J., Robert P. (2003) Ambulatory system for human motion analysis using a kinematic sensor: Monitoring of daily physical activity in the elderly. IEEE Transactions on Biomedical Engineering 50, 711-723. |
 Najafi B., Bharara M., Talal T.K., Armstrong D.G. (2012) Advances in balance assessment and balance training for diabetes. Diabetes Management 2, 293-308. |
 Najafi B., Crews R.T., Wrobel J.S. (2010) The importance of time spent standing for those at risk of diabetic foot ulceration. Diabetes Care 33, 2448-2450. |
 Najafi B., Helbostad J.L., Moe-Nilssen R., Zijlstra W., Aminian K. (2009) Does walking strategy in older people change as a function of walking distance. Gait and Posture 29, 261-266. |
 Najafi B., Miller D., Jarrett B.D., Wrobel J.S. (2010) Does footwear type impact the number of steps required to reach gait steady state?: an innovative look at the impact of foot orthoses on gait initiation. Gait and Posture 32, 29-33. |
 Riley P.O., Dicharry J., Franz J., Croce U.D., Wilder R.P., Kerrigan D.C. (2008) A kinematics and kinetic comparison of overground and treadmill running. Medicine and Science in Sports and Exercise 40, 1093-. |
 Russmann H., Salarian A., Aminian K., Villemure J., Burkhard P.R., Vingerhoets F.J. (2004) Longtem ambulatory gait monitoring in Parkinson's disease: Validation of a new wireless measurement system. Movement Disorders 19, S247-S247. |
 Schwenk M., Hauer K., Dutzi I., Mohler J., Najafi B. (2014) Predicting in-hospital falls in geriatric patients with dementia using one body-worn sensor. Journal of American Geriatrics Society 62, S146-S147. |
 Sell T.C., Tsai Y-S., Smoliga J.M., Myers J.B., Lephart S.M. (2007) Strength, flexibility, and balance characteristics of highly proficient golfers. The Journal of Strength and Conditioning Research 21, 1166-1171. |
 Toosizadeh N., Lei H., Schwenk M., Sherman S., Sternberg E., Mohler J., Najafi B. (2014a) Does integrative medicine enhance balance in aging adults? – Proof of concept for benefit of electro-acupuncture therapy in Parkinson’s Disease. Gerontology 61, 3-14. |
 Toosizadeh N., Mohler J., Wendel C., Najafi B. (2014b) Influences of frailty syndrome on open-loop and closed-loop postural control strategy. Gerontology 61, 51-60. |
 Tropp H., Askling C., Gillquist J. (1985) Prevention of ankle sprains. American Journal of Sports Medicine 13, 259-262. |
 Wikstrom E.A., Naik S., Lodha N., Cauraugh J. H. (2010) Bilateral balance impairments after lateral ankle trauma: a systematic review and meta-analysis. Gait and Posture 31, 407-414. |
 Winter D (1990) Biomechanics and motor control of human movement. New York. Wiley. |
 Wrobel J.S., Marclay S., Najafi B. (2012) Golfing skill level postural control differences: A brief report. Journal of Sports Science and Medicine 11, 452-458. |
|
| |
|
|
|
|

