|
|
|
| |
| ABSTRACT |
|
Tactics are one of the winning factors in table tennis matches because they can reflect the technical strength and strategies of players. However, the current evaluation method of tactics is relatively simple, and it can be difficult to distinguish the pros and cons of different tactics. To solve these issues, this study used information from 60 matches played by top-25 men’s right-handed shake-hand offensive players as samples and proposed a tactical benefit algorithm and a visible evaluation model to analyse tactical performance. The model could help coaches and players find meaningful tactics quickly and easily and make reasonable comparisons between them. The results showed that 1) the numbers of tactics based on the tactical association-mining model and the L-shaped curve were 37 in the first six strokes. Among them, there were 9 selected tactics in the first to third strokes, the third to fifth strokes, and the second to fourth strokes, respectively, and 10 selected tactics in the fourth to sixth strokes. 2) The visible evaluation model of tactical benefit can determine the difference between the frequency, scoring rate, and benefit of different tactics as mapped into the model as well as quickly and effectively discover the distribution of tactics and measure the advantages and disadvantages of tactics from multiple dimensions. |
| Key words:
Table tennis, tactical benefit, visible evaluation model, first six strokes, performance analysis
|
Key
Points
- The tactical benefit algorithm is the first attempt to measure the tactical features of the first six strokes in the service and receiving rounds based on the combination of the tactical frequency and scoring rate.
- Thirty-seven tactics based on the tactical association-mining model and the L-shaped curve are selected from the first six strokes of table tennis matches.
- The visible evaluation model of tactical benefit can determine the difference between the frequency, scoring rate, and benefit of different tactics.
|
Table tennis is a high-speed net sport that involves strong spin and many changes in techniques and tactics (Tian and Liu, 1985). Like all game sports, table tennis is a dynamic and interactive sport, and either side’s performance is influenced by that of the other side (Lames, 1991). The results of the matches will be affected by the performance of both sides, such as technical and tactical, psychological and physical aspects. Among them, techniques and tactics are the main influencing factors (Strauss and Arnold, 1987; McGarry and Franks, 1994; Hughes and Bartlett, 2002). Zhang et al. (2018) claimed that techniques and tactics are the key to winning matches and are widely studied factors in table tennis research. Wu et al. (1988) proposed a “three-phase evaluation method” for analysing the technical strength of table tennis players. According to the length of each rally in a game, three phases are classified (attack after service, attack after receiving, and stalemate), the usage and scoring rate of the phases are calculated, and the pro and cons of each phase are evaluated. The method is simple to understand and easy to use, and it has been quickly promoted and popularized in China (Hsu, 2010; Fuchs et al., 2018). With the development of computer and multimedia technology, coaches and players wanted to understand the details of tactics by players in the match instead of the strokes and phases. Therefore, various intelligent collection systems were constructed to record the stroke information, such as technique, placement, position, footwork types etc. (Zhang et al., 2010; Pradas et al., 2010, Malagoli et al., 2014); and a large number of mathematical models were used to analyse the tactics from different dimensions, such as Markov chain (Zhang and Hohmann, 2004; Pfeiffer et al., 2010), artificial neural network (Yang and Zhang, 2016), association mining (Zhang and Zhou, 2017) and game theory (Liu and Tang, 2013). In recent years, some systems based on visualization technology have been used in table tennis. Wu et al. (2018) proposed a novel interactive table tennis visualization system (iTTVis), which was used to analyse and explore table tennis tactical data and perform cross analysis to gain insights. Wang et al. (2019) constructed the Tac-Simur system, which is based on the characteristics of the Markov chain model, to characterize and simulate the effectiveness of the tactics used by different players. On this basis, Lan et al. (2021) explained the impact of the tactical adjustments that players make on different ball return techniques in terms of the scoring rate and proposed SimuExplorer, a visualization system to provide a multilevel analysis of these impacts. In addition, an interactive visualization system named Tac-Miner, which includes projection methods, was proposed to provide an overview of the massive high-dimensional technical and tactical data in table tennis. A comparative analysis of different tactics and a correlation analysis of adjacent tactics were also provided to determine the difference between tactics and assess and interpret the performance of the current tactic based on subsequent and previous tactics (Wang et al., 2021). The analysis of table tennis matches can be further studied in detail. For example, because the principle of the models and the results are too abstract, it is difficult for coaches and players to completely understand the effects of tactics and apply them in training and practice for competitions. Although Zhang et al. (2013) proposed a technical effectiveness formula and evaluation criteria to evaluate the technical strength of players, the method involved only "strokes" rather than specific stroke attributes, such as stroke technique, placement, and spin. Consequently, it is impossible to know what kind of tactics the players used or the effect of the tactics through the technical effectiveness formula. Therefore, we constructed a tactical benefit algorithm and a visible evaluation model with four classes to analyse the tactical performance of elite male players and help coaches and players easily and intuitively understand the nature of tactics and quickly distinguish the pros and cons of specific tactics. Match samplesIn this study, 60 matches of the top-25 men’s right-handed shake-hand offensive players were selected (based on the world ranking from 2016 to 2019). There were 29 players involved in total, including 17 Asian players, 9 European players, 2 African players and 1 South American player. The mean age, height and weight of the 29 players was 25.5 ± 4.8 years, 1.78 ± 0.08 m, and 69.7 ± 5.8 kg, respectively (data taken from the Wikipedia website). Information about the 60 matches is shown in Table 1. All match videos were taken from television relays or the internet. The study was approved by the local institutional ethics committee.
Observation indices and data collectionAccording to studies by Zhang and Zhou (2017) and Molodzoff (2008), the tactical observation indices included stroke technique, stroke placement, and rally results, as follows:
- Stroke technique:
-Serve, the first stroke used in each rally;
-Topspin (attack), an attacking stroke that imparts a topspin effect on the ball;
-Smash, an attacking stroke characterized by a linear trajectory and no spin of the ball;
-Flick, an attacking stroke performed when the ball bounces close to the net;
-Twist, an attacking stroke performed with a backhand flip when the ball bounces close to the net;
-Push, a controlling stroke that puts the ball to the bottom line of the table;
-Touch short, a controlling stroke that puts the ball close to the net;
-Block, a defensive stroke performed in response to an attacking stroke in a passive fashion;
-Lob, a defensive stroke performed when the player is far from the table, consisting of lifting the ball to a considerable height.
- Stroke placement: short forehand (SF), half long forehand (HLF), long forehand
(LF), short middle (SM), half long middle (HLM), long middle (LM), short backhand
(SB), half long backhand (HLB) and long backhand (LB).
- The rally results: scoring and losing.
In this study, two techniques (topspin and attack) are collectively referred to as the topspin (attack). This is because many elite players can strike the ball with both topspin and a high velocity; sometimes the technical movements of these two moves are quite close in appearance, so they are difficult to distinguish (Liu and Tang, 2013; Zhang and Zhou, 2017; Liu et al., 2022). Based on the above observation indices and the sequence of striking, the technique and placement of each stroke as well as the result of each rally were collected to meet the need of the analytical model. The objectivity of the observation indices was confirmed by the agreement of two independent observers using Cohen’s kappa statistic (interrater agreement) (Robson, 2002). Zhang and Zhou (2017) tested the objectivity of these observation indices and found that Cohen’s kappa value (k) was k = 0.995 for stroke technique, k = 0.992 for stroke placement and k = 1 for the rally results.
Tactical combination and its algorithmTactical combination
In this study, the tactical combination is composed of the different stroke techniques and stroke placements of three consecutive strokes by two players for the following reasons: (1) Stroke technique and placement are categorical variables, which have better operability and feasibility and can be formulated in advance according to the research needs by corresponding the observation indicators (systems) and operating rules. However, stroke rotation, speed and arc are continuous variables, and the data can only be obtained objectively and accurately through the use of eagle eye technology at matches or with the use of high-speed cameras, tachometers, speedometers and other equipment for testing in a laboratory environment. (2) As shown in previous studies, the outcome of the matches depends mainly on the performance of the first four strokes (Wu et al., 1988). Currently, the usage and point proportions of the fifth and sixth strokes were obviously higher than they were in previous matches (Jiang et al., 2011), and the relative tactical combinations had become more diverse. An increasing number of coaches and table tennis researchers proposed that the two strokes are drawn from the stalemate and combined with the third and fourth strokes to form a convergent tactic of the third to fifth strokes in the service round and the fourth to sixth strokes in the receiving round (Lan, 2014; Jiang and Yao, 2015). Therefore, this study mainly analysed the tactics combination of elite players in the first six strokes (the first to third strokes and the third to fifth strokes in the service round, and the second to fourth strokes and the fourth to sixth strokes in the receiving round).
Tactical frequency and scoring rate algorithmIn this study, the attributes of different strokes for each tactic are defined and computed first. Let X be a set of stroke techniques, Y be a set of stroke placements, D be a set of descriptive vectors of all rallies, Tn→n+2 be a set of tactical vectors of stroke n→n+2, and the value range of n be all positive integers. Among them, when n+2 exceeds the maximum number of strokes, Tn→n+2 is an empty set. A descriptive vector
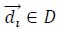 in a given rally can be shown as (
in a given rally can be shown as (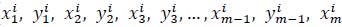 )
, where m represents the length, )
, where m represents the length, 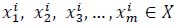 represents the stroke technique of strokes 1, 2, 3, …, m, and
represents the stroke technique of strokes 1, 2, 3, …, m, and
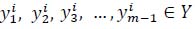 represents the stroke placement of strokes 1, 2, 3, …, m-1. In that rally (the sign of the end of the rally is that either side has lost a point, which means the loser has not returned the ball to the opponent's court, so the stroke placement does not exist). Then, the tactical vector
represents the stroke placement of strokes 1, 2, 3, …, m-1. In that rally (the sign of the end of the rally is that either side has lost a point, which means the loser has not returned the ball to the opponent's court, so the stroke placement does not exist). Then, the tactical vector
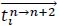 of stroke n→n+2 in that rally consists of
of stroke n→n+2 in that rally consists of
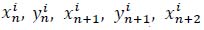 of the descriptive vector
of the descriptive vector
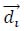 , in other words,
, in other words,
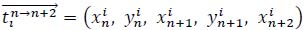 , among which n+2 is less than or equal to m.
, among which n+2 is less than or equal to m.
Let Nn→n+2 be the number of rallies in D that contain tactical vectors of stroke n→n+2. For any
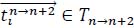 , let
, let
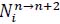 be the number of rallies that use tactical vector
be the number of rallies that use tactical vector
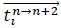 , let
, let
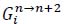 be the number of rallies that use tactical vector
be the number of rallies that use tactical vector
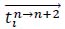 and finally score.
and finally score.
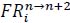 is defined as the frequency of tactical vector
is defined as the frequency of tactical vector
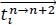 as well as a ratio of
as well as a ratio of
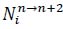 to
to
 .
.
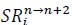 is defined as the scoring rate of tactical vector
is defined as the scoring rate of tactical vector
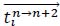 as well as a ratio of
as well as a ratio of
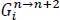 to
to
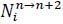 . Then,
. Then,
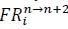 and
and
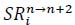 are computed by the following formulas.
are computed by the following formulas.
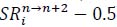 |
(1) |
| |
|
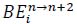 |
(2) |
Visible evaluation modelThe visible evaluation model of the tactical benefit is constructed in 7 steps:
Step 1: Make a scatter plot of the numbers of tactics in the first six strokes based on the tactical association-mining model and find that the scatter plot has L-shaped characteristics. To greatly affect the curve fitting by using formula 4, the tactics are divided by the quartile method, and 25% of them are eliminated.
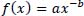 |
(4) |
In formula 4, a is positively related to the number of tactics, and b is related to the distribution of different tactics.
Step 2: In the L-shaped curve, the “steep” part of the function is large and representative, and the “flat” part of the function has adverse features. To find the representative tactics, it is necessary to find the part where the slope of the curve is relatively flat. Therefore, the derivative function formula 5 is obtained by taking the derivation of formula 4.
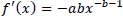 |
(5) |
Step 3: define “flat”. From formula 5, the curve is relatively flat when -abx-b-1>-k, and formula 6 can be obtained.
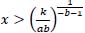 |
(6) |
Step 4: To meet the analysis needs of different rounds of tactics, formula 7 is derived, where x is the serial number of the tactical type, and tactics are filtered out when conforming to the needs of formula 8. In addition, the selected tactics are related to only b and c, and b is related to the distribution of tactics.
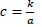 |
(7) |
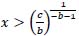 |
(8) |
Where a and b are constants over zero and c is a constant.
Step 5: In formula 8, the constant c needs to be determined. According to the different curvatures of the L-shaped curve fitting for the four-round tactics of elite male players, two values for constant c are obtained to determine the numbers of corresponding tactical types. Among them, c1 corresponds to the tactical numbers of the first to third strokes in the service round and the fourth to sixth strokes in the receiving round, and c2 corresponds to the tactical numbers of the third to fifth strokes in the service round and the second to fourth strokes in the receiving round. To ensure that the selected tactics are representative, 10±2 tactics should be obtained. According to the average of c1 and c2, the numbers of tactical types in each round are finally found, as shown in Figure 1.
Step 6: The tactical benefit derived from the median frequency and scoring rate of the selected tactics are used as the standard for dividing the four benefit class areas, which are first-class, second-class, third-class and fourth-class, and the ranges of the benefits of the selected tactics are [-Z, Z], where |Z| is less than 5. The tactical benefit BE (t) is as follows:
Step 7: The visible evaluation model of tactical benefit is constructed by taking the frequency and scoring rate of the selected tactics as the vertical and horizontal coordinates, respectively.
Basic dataIt is necessary to sort out the results of each stroke for elite male players because each tactic is composed of three strokes. Table 2 displays the results of each stroke for elite male players. Among them, the scoring rate of the third stroke is the highest (0.219) in the service round, followed by the fifth and first strokes (0.114). The scoring rate after the fifth strokes is only 0.079. In the receiving round, the second stroke has the highest scoring rate (0.203), followed by the fourth stroke (0.151), and the third is the sixth stroke (0.064). The scoring rate after the sixth strokes is the lowest (0.056). Since the direct scoring of the first and second strokes does not meet the definition of a tactic in this study (two consecutive strokes by a player constitute a tactic), the following analysis does not include the direct scoring of the first and second strokes.
Tactical features of the first to third strokes in the service roundFigure 2 displays the tactical benefits values and distribution of the first to third strokes in the visible evaluation model for elite male players as well as their scoring rate and frequency. For example, “tactic (T1): A Serve → SF, B Touch short → SM, A Push - - - > A Scoring” is a first-class benefit tactic in the first to third strokes, which can be understood as follows:
“Player A serves a ball to the short forehand, player B returns the ball with a touch short to short middle, then player A strikes the ball with a push; finally, player A scores in this rally (the strokes of the rally include player A scoring the point in the third and other strokes like the 5th, 7th, or 9th stroke, hereinafter the same).”
Figure 2 shows that the scoring rates of tactics (T1-T3) are over 0.5 and are also in the top 3 in the first to third strokes, which are 0.531, 0.523, and 0.509, respectively. Based on their tactical frequency (0.029, 0.022, and 0.037), tactic (T1) is the only first-class benefit tactic (0.090), tactics (T2) and (T3) are second-class benefit tactics, and the values are 0.050 and 0.033. The third-class benefit tactics (T4-T6) are below zero, as are those of fourth-class benefit tactics (T7-T9). Among them, tactic (T9) has the lowest benefit (-0.362) as well as the scoring rate (0.383), and the frequency is 0.031. The benefit of the tactic (T8) is -0.281, which has the highest frequency (0.067) but a lower scoring rate (0.458).
Tactical features of the third to fifth strokes in the service roundFigure 3 displays the tactical benefits values and distribution of the third to fifth strokes in the visible evaluation model for elite male players as well as their scoring rate and frequency. For example, “tactic (T10): (LB), A Topspin (Attack) → LM, B Block → LB, A Topspin (Attack) - - - > A Scoring” is a first-class benefit tactic in the third to fifth strokes, which can be understood as follows:
“(Player B returns a ball to the long backhand), player A strikes the ball with topspin (attack) to the long middle, player B strikes the ball with block to the long backhand, player A strikes the ball with a topspin (attack); finally player A scores in this rally (the strokes of the rally include player A scoring the point in the fifth and other strokes like the 7th, or 9th stroke, hereinafter the same).”
Figure 3 shows that the scoring rates of tactics (T10-T14) are all over 0.5, even though those of tactics (T10-T12) are over 0.6 (0.684 and 0.651). Among them, the first four tactics are first-class benefit tactics, and the ranges of the benefit and scoring rate are 0.078 to 0.409 and 0.530 to 0.684, respectively. Tactic (T14) is a second-class benefit tactic (0.039) because it has the lowest frequency (0.015) and the scoring rate is not too high (0.526). Tactics (T15-T18) are fourth-class benefit tactics, and the benefits are negative, from -0.467 to -0.058. Of course, their scoring rates are also under 0.5. Tactic (T17) has the lowest scoring rate (0.377), followed by tactic (T18), for which the scoring rate is 0.380, but has the highest frequency (0.039) in the third to fifth strokes.
Tactical features of the second to fourth strokes in the receiving roundFigure 4 shows the tactical benefit, scoring rate, and frequency of tactics in the second to fourth strokes for elite male players. Tactic (T19) has the highest scoring rate (0.591) and relatively higher frequency (0.012), so named the first-class benefit tactic and the value is 0.105. The benefit of the tactic (T20) is 0.044 and it can almost be a first-class benefit tactic if the scoring rate (0.529) or frequency (0.015) increases slightly. Tactic (T22) has the highest frequency (0.019), but the benefit is negative (-0.026) because its scoring rate is less than 0.5 (0.486). Tactic (T26) has the lowest scoring rate (0.326), and the frequency and benefit are 0.011 and -0.197, respectively. Tactic (T27) has the same benefit as a tactic (T26) but differs in scoring rate and frequency (0.340 and 0.012).
Tactical features of the fourth to sixth strokes in the receiving roundFigure 5 presents ten tactics with benefit, scoring rate, and frequency of the fourth to sixth strokes in the receiving round. The second-class benefit tactic (T28) has the highest scoring rate, frequency, and benefit, which are 0.537, 0.031, and 0.117, respectively, followed by the tactic (T29), the values are 0.511, 0.026, and 0.029, respectively. The scoring rate of tactics (T30-T37) is less than 0.5 so their benefits are negative and the range is -0.262 to -0.087. Tactics (T30-T33) are third-class benefit tactics, and the other tactics are fourth-class benefit tactics. In addition, the tactic (T35-T37) has the same benefit (-0.262) but different scoring rate and frequency, which are 0.390, 0.395, 0.333 and 0.024, 0.025, 0.016, respectively.
Scoring rate of strokes in the service and receivingroundsThe results show that the main points of the elite male players are in the first four strokes of the service and receiving rounds in Table 2. The reason is that elite male players are good at using high-quality serve and strike with offensive techniques in the third stroke. When returning a ball, they also attack first and offense in the next stroke consecutively. In addition, the scoring rate declines with the increase in the number of strokes, except for the first stroke. This illustrates that each scoring advantage of a stroke diminishes as it passes to the next stroke (Tamaki et al, 2017; Zhou and Zhang, 2019).
Features of the first six stroke tactics in the service and receiving roundsThe visible evaluation model of the tactical benefit can supply direct and rapid judgement on various tactics for coaches and players. For example, In Figure 2, Figure 3 and Figure 4, the results intuitively show that players will become relatively more effective when serving or controlling a ball to short forehand (middle) and attack first in the next stroke with topspin (attack). On the contrary, being attacked by the opponent to long backhand first, will lead some worse effectiveness in generally as well as returning the ball with push to long backhand and defense in the fourth stroke. A similar opinion was proposed by Zhang and Zhou (2017). There are also some different views. We think it would be a good tactic that player controls the ball to short and not let the opponent attack first, such as the first-class benefit tactic (T19) in the second to fourth strokes, but the tactics (T4), (T8) and (T23) in the first to third strokes and the second to fourth strokes show the opposite results. It may be that these tactics are overused and adapted by opponents, leading to diminishing marginal returns in scoring rates and tactical benefits. Here is one more first-class benefit tactic (T1) worth noting: pushing to long actively after the opponent returns the ball to short, although their frequency is not relatively high in the first to third strokes. This seems to be explained as a new type of tactic that player pushes a ball to long initiative after serving, and forces the opponent strikes with topspin or push back in normal quality, then the player attacks back strongly with full preparation in the fifth stroke. However, the frequency of such tactics may be too low to be shown in the current study. The main tactics in Figure 3 show that when a player continuously attacks the long backhand (middle), the more times the opponent chooses defending instead of attacking to long middle (backhand) in the fourth stroke (T10, T11 and T12), the relatively better the scoring rate and benefit of tactics will be, and no matter what the frequency of tactics are. However, the tactics that elite male players strike the ball with topspin (attack) against topspin (attack) to long backhand (middle) (T35-T37) are not as advantageous as the similar tactics in Figure 5. This means that the benefits of such tactics are uncertain and largely depends only on the stalemate strength of the players on both sides. Some tactics of the fourth to sixth strokes have the most obvious disadvantage in Figure 5. These tactics show that the player strikes a ball with topspin (attack) in the sixth stroke after blocking to long middle (backhand) in the fourth stroke and the opponent strikes the ball with topspin (attack) to long backhand (middle) in the fifth stroke (T31, T33 and T34). Therefore, the proverb, “gain mastery by striking only after the enemy has struck”, does not work in the table tennis match.
Comparison of tactics selected and tactical benefit formulasIn other studies, the criteria for selecting tactics to analyse are as follows: several tactics are regarded as the most representative according to the frequency of different tactics or tactics selected with a certain frequency for analysis according to tactics in the different rounds (Zhang and Zhou, 2017). In this study, the relatively reasonable way to choose which tactics to analyse is to find the inflection point (as the tactics) from steep to relatively flat in the L-shaped curve of the scatter plot. Comparing the tactical benefit formula with the technical effectiveness formula proposed by Zhang et al. (2013), we find that both meet the basic requirements of tactical or technical benefit for table tennis matches. The similarities are as follows:
- When the scoring rate is over 0.5, the higher the frequency or usage rate, the higher the tactical benefit or technical effectiveness;
- When the scoring rate is under 0.5, the higher the frequency or usage rate, the lower the tactical benefit or technical effectiveness;
- When the scoring rate is equal to 0.5, regardless of how the frequency and usage rate change, the tactical benefit or technical effectiveness value remains unchanged.
The differences of both formulas can be seen:
- The technical effectiveness formula
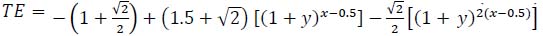 was obtained by using a quadratic function of TE0 to fit the three pairs of data of TE0 and TE, where TE represents the technical effectiveness, y represents the usage rate, and x represents the scoring rate of certain techniques. However, it is difficult for people to understand how the constant
was obtained by using a quadratic function of TE0 to fit the three pairs of data of TE0 and TE, where TE represents the technical effectiveness, y represents the usage rate, and x represents the scoring rate of certain techniques. However, it is difficult for people to understand how the constant
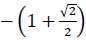 and coefficients 1.5+√2 and
and coefficients 1.5+√2 and
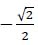 are derived and what they mean. The tactical benefit formula
are derived and what they mean. The tactical benefit formula
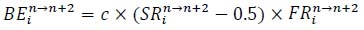 is based on the scoring rate
is based on the scoring rate
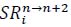 and frequency
and frequency
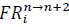 of certain tactics in the n→n+2 stroke and a constant c. The pure formula of the tactical benefit can be simplified as BEi=c×(SRi-0.5)×FRi if all n→n+2 strokes are not considered in the formula. Therefore, it is easier to understand the tactical benefit formula than the technical effectivenss formula.
of certain tactics in the n→n+2 stroke and a constant c. The pure formula of the tactical benefit can be simplified as BEi=c×(SRi-0.5)×FRi if all n→n+2 strokes are not considered in the formula. Therefore, it is easier to understand the tactical benefit formula than the technical effectivenss formula.
- The tactical benefit formula has positive and negative values when the value of
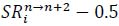 is over or under zero. It provides coaches and players with more intuitive experience than the technical effectiveness formula, which yields a range of values of the form [0, 1]. In addition, the tactical benefits can be adjusted appropriately according to the needs of research because of the constant c, and it is more flexible than the technical effectiveness formula.
is over or under zero. It provides coaches and players with more intuitive experience than the technical effectiveness formula, which yields a range of values of the form [0, 1]. In addition, the tactical benefits can be adjusted appropriately according to the needs of research because of the constant c, and it is more flexible than the technical effectiveness formula.
- In the tactical benefit formula, when FRi is equal to 0, BEi will always be equal to 0. However, in the technical effectiveness formula, when y (usage rate) is equal to 0, TE will always be equal to 0.5. This shows that the former is more reasonable than the latter, since a certain technique should not show technical effectiveness if it is not used.
The practical application of the visible evaluation model of the tactical benefitFigure 6 shows the most frequently used tactics and their characteristics in the visible evaluation model for the second to fourth strokes of the receiving round by a Chinese player, who was against other countries' elite players in ten matches (2017-2019). Among them, tactic (T38) has the highest scoring rate, reaching 1, and the benefit value is 1.085. Following tactics (T39) and (T40), the scoring rates are 0.714 and 0.556, respectively, and they are all first-class benefit tactics. In addition, the scoring rates of tactics (T41) and (T42) are less than 0.5, which are 0.375 and 0.286, respectively. According to the criteria of the visible evaluation model, these two tactics are fourth-class benefit tactics (the values are -0.310 and -0.465, respectively). The results show that striking with a twist combined with the continuous attack in the fourth stroke was his main scoring method. However, the tactics for defencing in the fourth stroke are not effective. Therefore, in the next matches, the coaches formulate for the player that the main tactical combination of the second and fourth strokes is twist first and topspin (attack) in the fourth stroke and strengthen the ability of the fourth stroke to actively counter the opponent. The player will use this tactical combination more positively in the matches and reduce the frequency of those tactics that include the strokes of control and passive defense. For physical trainers, it is necessary to continue to strengthen the footwork movement of stepping forward and then stepping back and the practice of continuous attacking during the movement.
Limitation and outlookMolodzoff (2008) mentioned that the topspin (abbreviated as top) and top counter top (a counterattacking stroke consisting of a top performed against an opponent’s top) were different stroke types, which can more accurately and comprehensively reflect the technical characteristics of players. However, to make the tactical combination data easier to cluster and clearly display the tactical characteristics, the above two techniques were combined into topspin (attack) as one stroke technique in the data collection of this study. We hope that with the increase in data, the topspin and top counter top can be distinguished and studied specifically in future research. The types and benefits of tactics in the visible evaluation model often depend on the matches’ samples. Different match samples, such as different match events, different genders, different play styles, and different gripping methods, will make the tactical characteristics, benefits, and evaluation standards changed. Therefore, these also need to be gradually improved in future research work so that coaches and players can better understand and master the tactical characteristics in different ways. Table tennis, badminton, tennis, and volleyball belong to skill-led cross-net competitions. The course of the match can be regarded as a natural time sequence. At the end of a round, there are only two results, namely, score or loss. Therefore, the visible evaluation model of tactical benefit in this study is also applicable to the tactical analysis of badminton, tennis, and volleyball as long as the researchers change the indices of collection and analysis.
In this study, we establish the problem of tactical benefit in table tennis matches. To solve this problem, we introduce a tactical benefit algorithm and a visible evaluation model with four classes. The tactical benefit algorithm is the first attempt to measure the tactical features of the first six strokes in the service and receiving rounds based on the combination of the tactical frequency and scoring rate. The visible evaluation model for the tactical benefit problem can help coaches and players assess the difference between the frequency, scoring rate, and benefit of different tactics as mapped into the model as well as quickly and effectively discover the distribution of tactics and measure the advantages and disadvantages of tactics from multiple dimensions.
| ACKNOWLEDGEMENTS |
The experiments complied with the current laws of the country in which they were performed. The authors have no conflicts of interest to declare. The datasets generated and analyzed during the current study are not publicly available, but are available from the corresponding author who was an organizer of the study. |
|
| AUTHOR BIOGRAPHY |
|
 |
Zheng Zhou |
| Employment: Department of Sport Science, College of Education, Zhejiang University |
| Degree: PhD |
| Research interests: Technique and tactic analysis in table tennis, data analysis in sport |
| E-mail: zheng.zhou@zju.edu.cn |
| |
 |
Hui Zhang |
| Employment: Department of Sport Science, College of Education, Zhejiang University |
| Degree: PhD |
| Research interests: Training science, match analysis, performance analysis |
| E-mail: zhang_hui@zju.edu.cn |
| |
|
| |
| REFERENCES |
 Fuchs M., Liu R., Lanzoni I. M., Munivrana G., Straub G., Tamaki S., Yoshida K., Zhang H., Lames M. (2018) Table tennis match analysis: A review. Journal of Sports Sciences 36, 1-10. Crossref |
 Hsu M.H. (2010) A study on the technical analysis and attack-defense performance of men’s top four single players in 2008 Olympic Games. International Journal of Table Tennis Sciences 6, 248-260.
https://sasportssience.blob.core.windows.net/ijtts/IJTTS_6_pdf%20files/IJTTS_6_248_260_Hsu_A%20study.pdf |
 Hughes M. D., Bartlett R. M. (2002) The use of performance indicators in performance analysis. Journal of Sports Sciences 20, 739-754. Crossref |
 Jiang J., Li Z., Xu J. (2011) Technique and tactic analysis of China's women table tennis team in the 50th world table tennis championship. Journal of Beijing Sport University 34, 142-144. Crossref |
 Jiang J., Yao J. (2015) Evaluation on tactical skills in table tennis single match and reconstruction and applications of its diagnostic methods. Journal of Tianjin University of Sport 30, 432-437. Crossref |
 Lames, M. (1991) Leistungsdiagnostik durch Computersimulation [Performance analysis by computer simulation]. Frankfurt/Main:
Harri Deutsch. |
 Lan J., Zhou Z., Wang J., Zhang H., Xie X., Wu Y. (2021) SimuExplorer: visual exploration of game simulation in table tennis. IEEE Transactions on Visualization and Computer Graphics. Crossref |
 Lan T. (2014) Commentary on men’s singles final of table tennis in the 12 national games and research on the dynamics of forward position of its techniques and tactics. China Sport Science and Technology 50, 57-61. Crossref |
 Liu W., Tang J. (2013) Theory and empirical research of table tennis tactical behavior based on game theory. Journal of Beijing Sport University 36, 119-124. Crossref |
 Liu W., Zhou Z., Shen Y., Zhang H. (2022) Stroke performance relevance model for elite table tennis matches. International Journal of Performance Analysis in Sport. Crossref |
 Malagoli Lanzoni I., Di Michele R., Merni F. (2014) A notational analysis of shot characteristics in top-level table tennis players. European Journal of Sport Science 14, 309-317. Crossref |
 McGarry T., Franks I. M. (1994) A stochastic approach to predicting competition squash match-play. Journal of Sports Sciences 12, 573-584. Crossref |
 Molodzoff, P. (2008). ITTF Advanced Coaching Manual (p. 105-107). Lausanne: International Table Tennis Federation. |
 Pfeiffer M., Zhang H., Hohmann A. (2010) A Markov chain model of elite table tennis competition. International Journal of Sports Science and Coaching 5, 205-222. Crossref |
 Pradas F., Floría P., Carrasco L., Beamonte A., González J. A., Mu T. (2010) Design and development of an observational tool for evaluating table tennis singles matches. International Journal of Table Tennis Sciences 6, 181-186.
https://sasportssience.blob.core.windows.net/ijtts/IJTTS_6_pdf%20files/IJTTS_6_181_185_Pradas_Design.pdf |
 Robson, C. (2002). Real world research (2nd ed.). Oxford: Blackwell. |
 Strauss D., Arnold B. C. (1987) The rating of players in racquetball tournaments. Journal of the Royal Statistical Society. Series C (Applied Statistics) 36, 163-173. Crossref |
 Tamaki S., Yoshida K., Yamada K. (2017) A shot number based approach to performance analysis in table tennis. Journal of Human Kinetics 55, 7-18. Crossref |
 Tian M., Liu X. (1985) Research on the classification of competitive sports. Journal of Beijing Sport University 1, 63-75. Crossref |
 Wang J., Wu J., Cao A., Zhou Z., Zhang H., Wu Y. (2021) Tac-miner: visual tactic mining for multiple table tennis matches. IEEE Transactions on Visualization and Computer Graphics 27, 2770-2782. Crossref |
 Wang J., Zhao K., Deng D., Cao A., Xie X., Zhou Z., Zhang H., Wu Y. (2019) Tac-simur: tactic-based simulative visual analytics of table tennis. IEEE Transactions on Visualization and Computer Graphics 26, 407-417. Crossref |
 Wu H., Wu H. O., Cai X., Sun Q., Wang S., Chen M. (1988) Strength evaluation and technique analysis on Chinese players in table tennis matches of the 1988 Olympic Games. China Sport Science and Technology 8, 34-49. Crossref |
 Wu Y., Lan J., Shu X., Ji C., Zhao K., Wang J., Zhang H. (2018) iTTVis: Interactive visualization of table tennis data. IEEE Transactions on Visualization and Computer Graphics 24, 709-718. Crossref |
 Yang Q., Zhang H. (2016) Application of BP neural network and multiple regression in table tennis technical and tactical ability analysis. Journal of Chengdu Sport University 42, 78-82. Crossref |
 Zhang H., Hohmann A. (2004) Athletic diagnosis of table tennis matches through mathematic simulation. Journal of Shanghai Physical Education Institute 28, 68-72. Crossref |
 Zhang H., Liu W., Hu J., Liu R. (2013) Evaluation of elite table tennis players’ technique effectiveness. Journal of Sports Sciences 31, 1526-1534. Crossref |
 Zhang H., Yu L., Hu J. (2010) Computer-aided game analysis of net sports in preparation of Chinese teams for Beijing Olympics. International Journal of Computer Science in Sport 9, 53-69.
https://iacss.org/fileadmin/user_upload/IJCSS_Abstracts/Vol9_Ed3/IJCSS-Volume9_Edition3_Abstract_Hui.pdf |
 Zhang H., Zhou Z. (2017) An analytical model of the two basic situation strategies in table tennis. International Journal of Performance Analysis in Sport 17, 970-985. Crossref |
 Zhang H., Zhou Z., Yang Q. (2018) Match analysis of table tennis in China: a systematic review. Journal of Sports Sciences 36, 2663-2674. Crossref |
 Zhou X., Zhang Y. (2019) Exploration about the competitive performance and countermeasures of table tennis based on board characteristics in the context of the new ball era. Journal of Tianjin University of Sport 34, 165-171. Crossref |
|
| |
|
|
|
|

